
°æƒø°øƒ≥∏€ø⁄”–“ª∏ˆ≤¥Œª£¨œ÷Õ≥º∆¡Àƒ≥100À“¬÷¥¨‘⁄∏√≤¥ŒªÕ£øøµƒ ±º‰£®µ•Œª£∫–° ±£©£¨»Áπ˚Õ£øø ±º‰≤ª◊„∞Ζ° ±∞¥∞Ζ° ±º∆ ±£¨≥¨π˝∞Ζ° ±≤ª◊„1–° ±∞¥1–° ±º∆ ±£¨“‘¥À¿ýÕ∆£¨Õ≥º∆Ω·π˚»Áœ¬±Ì£∫

£®1£©…Ë∏√‘¬100À“¬÷¥¨‘⁄∏√≤¥Œªµƒ∆Ωæ˘Õ£øø ±º‰Œ™![]() –° ±£¨«Û
–° ±£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©ºŸ∂®ƒ≥ÃÏ÷ª”–º◊°¢““¡ΩÀ“¬÷¥¨–Ë“™‘⁄∏√≤¥ŒªÕ£øø![]() –° ±£¨«“‘⁄“ª÷Á“𵃠±º‰∂Œ÷–Àʪ˙µΩ¥Ô£¨«Û’‚¡ΩÀ“¬÷¥¨÷¡…Ÿ”–“ªÀ“‘⁄Õ£øø∏√≤¥Œª ±±ÿ–廥˝µƒ∏≈¬ .
–° ±£¨«“‘⁄“ª÷Á“𵃠±º‰∂Œ÷–Àʪ˙µΩ¥Ô£¨«Û’‚¡ΩÀ“¬÷¥¨÷¡…Ÿ”–“ªÀ“‘⁄Õ£øø∏√≤¥Œª ±±ÿ–廥˝µƒ∏≈¬ .
°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£©![]() .
.
°æΩ‚Œˆ°ø
£®1£©¿˚”√◊Ð ±º‰≥˝“‘![]() «Ûµ√∆Ωæ˘Õ£øø ±º‰
«Ûµ√∆Ωæ˘Õ£øø ±º‰![]() .£®2£©…Ë≥ˆº◊““¡Ω¥¨µΩ¥Ôµƒ ±º‰£¨”…£®1£©¡–≥ˆ≤ªµ» Ω
.£®2£©…Ë≥ˆº◊““¡Ω¥¨µΩ¥Ôµƒ ±º‰£¨”…£®1£©¡–≥ˆ≤ªµ» Ω![]() £¨ª≠≥ˆø…––”Ú∫Û£¨¿˚”√√ʪ˝µƒ±»«Ûµ√–Ë“™µ»¥˝µƒ∏≈¬ .
£¨ª≠≥ˆø…––”Ú∫Û£¨¿˚”√√ʪ˝µƒ±»«Ûµ√–Ë“™µ»¥˝µƒ∏≈¬ .
Ω‚£∫£®1£©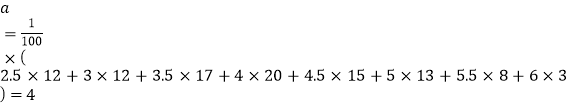 .
.
£®2£©…˺◊¥¨µΩ¥Ôµƒ ±º‰Œ™![]() £¨““¥¨µΩ¥Ôµƒ ±º‰Œ™
£¨““¥¨µΩ¥Ôµƒ ±º‰Œ™![]() £¨
£¨
‘Ú![]()
»Ù’‚¡ΩÀ“¬÷¥¨‘⁄Õ£øø∏√≤¥Œª ±÷¡…Ÿ”–“ªÀ“–Ë“™µ»¥˝£¨
‘Ú![]() £¨
£¨
∑˚∫œÃ‚“‚µƒ«¯”ÚŒ™“ı”∞≤ø∑÷£®≤ª∞¸¿®![]() £¨
£¨![]() ÷·£©£¨
÷·£©£¨
º«°∞’‚¡ΩÀ“¥¨‘⁄Õ£øø∏√≤¥Œª ±÷¡…Ÿ”–“ªÀ“¥¨–Ë“™µ»¥˝°±Œ™ ¬º˛![]() £¨
£¨
‘Ú![]() .
.
¥£∫’‚¡ΩÀ“¬÷¥¨÷–÷¡…Ÿ”–“ªÀ“‘⁄Õ£øø∏√≤¥Œª ±±ÿ–廥˝µƒ∏≈¬ Œ™![]() .
.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬±Ì «ƒ≥µÿƒ≥ƒÍ‘¬∆Ωæ˘∆¯Œ¬£®ª™ œ∂»£©£∫
‘¬∑ð | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
∆Ωæ˘∆¯Œ¬ | 21.4 | 26.0 | 36.0 | 48.8 | 59.1 | 68.6 | 73.0 | 71.9 | 64.7 | 53.5 | 39.8 | 27.7 |
“‘‘¬∑ðŒ™x÷·£®![]() ‘¬∑ð
‘¬∑ð![]() £©£¨“‘∆Ωæ˘∆¯Œ¬Œ™y÷·.
£©£¨“‘∆Ωæ˘∆¯Œ¬Œ™y÷·.
£®1£©”√’˝œ“«˙œþ»•ƒ‚∫œ’‚–© ˝æð£ª
£®2£©π¿º∆’‚∏ˆ’˝œ“«˙œþµƒ÷Ð∆⁄T∫Õ’Ò∑˘A£ª
£®3£©œ¬√Ê»˝∏ˆ∫Ø ˝ƒ£–Õ÷–£¨ƒƒ“ª∏ˆ◊Ó ∫œ’‚–© ˝æð£ø
¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª¢€
£ª¢€![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ◊Û°¢”“∂•µ„∑÷±Œ™
µƒ◊Û°¢”“∂•µ„∑÷±Œ™![]() £¨
£¨![]() £¨«““‘œþ∂Œ
£¨«““‘œþ∂Œ![]() Œ™÷±æ∂µƒ‘≤”Î÷±œþ
Œ™÷±æ∂µƒ‘≤”Î÷±œþ![]() œý«–£¨Õ÷‘≤
œý«–£¨Õ÷‘≤![]() Ωÿ÷±œþ
Ωÿ÷±œþ![]() À˘µ√œþ∂Œµƒ≥§∂»Œ™1.
À˘µ√œþ∂Œµƒ≥§∂»Œ™1.
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©…Ëπ˝µ„![]() µƒ∂Ø÷±œþ
µƒ∂Ø÷±œþ![]() ”ÎÕ÷‘≤
”ÎÕ÷‘≤![]() œýΩª”⁄
œýΩª”⁄![]() £¨
£¨![]() ¡Ωµ„£¨»Ù
¡Ωµ„£¨»Ù![]() £®
£®![]() Œ™◊¯±Í‘≠µ„£©£¨«Û÷±œþ
Œ™◊¯±Í‘≠µ„£©£¨«Û÷±œþ![]() µƒ–±¬ µƒ»°÷µ∑∂Œß.
µƒ–±¬ µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Ù’˚ ˝![]() °¢
°¢![]() º»≤ªª•Àÿ£¨”÷≤ª¥Ê‘⁄’˚≥˝πÿœµ£¨‘Ú≥∆
º»≤ªª•Àÿ£¨”÷≤ª¥Ê‘⁄’˚≥˝πÿœµ£¨‘Ú≥∆![]() °¢
°¢![]() Œ™“ª∏ˆ°∞¡™√À°± ˝∂‘.…Ë
Œ™“ª∏ˆ°∞¡™√À°± ˝∂‘.…Ë![]() Œ™ºØ
Œ™ºØ![]() µƒ
µƒ![]() ‘™◊”ºØ£¨«“
‘™◊”ºØ£¨«“![]() ÷–»Œ¡Ω ˝æ˘Œ™¡™√À ˝∂‘.«Û
÷–»Œ¡Ω ˝æ˘Œ™¡™√À ˝∂‘.«Û![]() µƒ◊Ó¥Û÷µ
µƒ◊Ó¥Û÷µ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…ËaŒ™ µ ˝£¨∫Ø ˝f£®x£©=ex©Å2x+2a£¨x° R£Æ
£®1£©«Ûf£®x£©µƒµ•µ˜«¯º‰º∞º´÷µ£ª
£®2£©«Û÷§£∫µ±a£æln2©Å1«“x£æ0 ±£¨ex£æx2©Å2ax+1£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £¨
£¨![]() .
.
£®1£©»Ù∫Ø ˝![]() ‘⁄
‘⁄![]() ¥¶µƒ«–œþ”Î÷±œþ
¥¶µƒ«–œþ”Î÷±œþ![]() ∆Ω––£¨«Û µ ˝
∆Ω––£¨«Û µ ˝![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£© ‘Ã÷¬€∫Ø ˝![]() ‘⁄«¯º‰
‘⁄«¯º‰![]() …œµƒ◊Ó¥Û÷µ£ª
…œµƒ◊Ó¥Û÷µ£ª
£®3£©»Ù![]() ±£¨∫Ø ˝
±£¨∫Ø ˝![]() «°”–¡Ω∏ˆ¡„µ„
«°”–¡Ω∏ˆ¡„µ„![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄ ˝¡–![]() £¨
£¨![]() ÷–£¨“—÷™
÷–£¨“—÷™![]() £¨
£¨![]() £¨«“
£¨«“![]() £¨
£¨![]() £¨
£¨![]() ≥…µ»≤Ó ˝¡–£¨
≥…µ»≤Ó ˝¡–£¨![]() £¨
£¨![]() £¨
£¨![]() “≤≥…µ»≤Ó ˝¡–£Æ
“≤≥…µ»≤Ó ˝¡–£Æ
![]() «Û÷§£∫
«Û÷§£∫![]() «µ»±» ˝¡–£ª
«µ»±» ˝¡–£ª
![]() …Ëm «≤ª≥¨π˝100µƒ’˝’˚ ˝£¨«Û π
…Ëm «≤ª≥¨π˝100µƒ’˝’˚ ˝£¨«Û π![]() ≥…¡¢µƒÀ˘”– ˝∂‘
≥…¡¢µƒÀ˘”– ˝∂‘![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ÷Ω´ƒ≥–£∏þ∂˛ƒÍº∂ƒ≥∞ýµƒ—ß“µÀÆ∆Ω≤‚ ‘ ˝—ß≥…º®∑÷Œ™![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() ŒÂ◊È£¨ªÊ÷∆∂¯≥…µƒæ•“∂Õº°¢∆µ¬ ∑÷≤º÷±∑ΩÕº»Áœ¬£¨”…”⁄π§◊˜ Ë∫ˆ£¨æ•“∂Õº”–≤ø∑÷±ªÀªµ£¨∆µ¬ ∑÷≤º÷±∑ΩÕº“≤≤ªÕÍ’˚£¨«Îæð¥ÀΩ‚¥»Áœ¬Œ £∫£®◊¢£∫∏√∞ýÕ¨—ß ˝—ß≥…º®æ˘‘⁄«¯º‰
ŒÂ◊È£¨ªÊ÷∆∂¯≥…µƒæ•“∂Õº°¢∆µ¬ ∑÷≤º÷±∑ΩÕº»Áœ¬£¨”…”⁄π§◊˜ Ë∫ˆ£¨æ•“∂Õº”–≤ø∑÷±ªÀªµ£¨∆µ¬ ∑÷≤º÷±∑ΩÕº“≤≤ªÕÍ’˚£¨«Îæð¥ÀΩ‚¥»Áœ¬Œ £∫£®◊¢£∫∏√∞ýÕ¨—ß ˝—ß≥…º®æ˘‘⁄«¯º‰![]() ƒ⁄£©
ƒ⁄£©

£®1£©Ω´∆µ¬ ∑÷≤º÷±∑ΩÕº≤π≥‰ÕÍ’˚£Æ
£®2£©∏√∞ýœ£Õ˚◊ÈΩ®¡Ω∏ˆ ˝—ß—ßœ∞ª•÷˙–°◊È£¨∞ý…œ ˝—ß≥…º®◊Ó∫√µƒ¡ΩŒªÕ¨—ß∑÷±µ£»Œ¡Ω◊È◊È≥§£¨Ω´¥À¥Œ≥…º®µÕ”⁄60∑÷µƒÕ¨—ß◊˜Œ™◊È‘±∆Ωæ˘∑÷µΩ¡Ω◊È£¨º¥√ø◊È”–“ª√˚◊È≥§∫Õ¡Ω√˚≥…º®µÕ60∑÷µƒ◊È‘±£¨«Û¥À¥Œøº ‘≥…º®Œ™52∑÷°¢54∑÷∫Õ98∑÷µƒ»˝√˚Õ¨—ß∑÷µΩÕ¨“ª◊ȵƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]()
£®1£©«Û∫Ø ˝![]() µƒµ•µ˜«¯º‰£ª
µƒµ•µ˜«¯º‰£ª
£®2£©…Ë![]() £¨»Ù∂‘»Œ“‚
£¨»Ù∂‘»Œ“‚![]() £¨≤ªµ» Ω
£¨≤ªµ» Ω![]() ∫„≥…¡¢£¨«Û µ ˝
∫„≥…¡¢£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com