
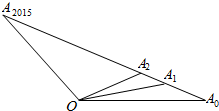
 ��ͼ��OΪֱ��A0A2015��һ�㣬��A0��A1��A2��A3��A4��A5������A2015��������������ľ�����ȣ���$\overrightarrow{O{A}_{0}}$=$\overrightarrow{a}$��$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$����$\overrightarrow{a}$��$\overrightarrow{b}$��ʾ$\overrightarrow{O{A}_{0}}$+$\overrightarrow{O{A}_{1}}$+��+$\overrightarrow{O{A}_{2015}}$������Ϊ1008��$\overrightarrow{a}$+$\overrightarrow{b}$����
��ͼ��OΪֱ��A0A2015��һ�㣬��A0��A1��A2��A3��A4��A5������A2015��������������ľ�����ȣ���$\overrightarrow{O{A}_{0}}$=$\overrightarrow{a}$��$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$����$\overrightarrow{a}$��$\overrightarrow{b}$��ʾ$\overrightarrow{O{A}_{0}}$+$\overrightarrow{O{A}_{1}}$+��+$\overrightarrow{O{A}_{2015}}$������Ϊ1008��$\overrightarrow{a}$+$\overrightarrow{b}$���� ���� ��DΪA0��A2015���е㣬������ɵ�$\overrightarrow{O{A}_{0}}$+$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{a}$+$\overrightarrow{b}$=2$\overrightarrow{OD}$��$\overrightarrow{O{A}_{1}}$+$\overrightarrow{O{A}_{2014}}$=2$\overrightarrow{OD}$����$\overrightarrow{O{A}_{1007}}$+$\overrightarrow{O{A}_{1008}}$=2$\overrightarrow{OD}$������ʽ����ӿɵã�
��� �⣺��DΪA0��A2015���е㣬
������ɵ�$\overrightarrow{O{A}_{0}}$+$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{a}$+$\overrightarrow{b}$=2$\overrightarrow{OD}$
ͬ���ɵ�$\overrightarrow{O{A}_{1}}$+$\overrightarrow{O{A}_{2014}}$=2$\overrightarrow{OD}$��
��
$\overrightarrow{O{A}_{1007}}$+$\overrightarrow{O{A}_{1008}}$=2$\overrightarrow{OD}$��
��$\overrightarrow{O{A}_{0}}$+$\overrightarrow{O{A}_{1}}$+��+$\overrightarrow{O{A}_{2015}}$=$\frac{2016}{2}$•2$\overrightarrow{OD}$=1008��$\overrightarrow{a}$+$\overrightarrow{b}$��
�ʴ�Ϊ��1008��$\overrightarrow{a}$+$\overrightarrow{b}$��
���� ���⿼�������������η����������⣮


 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5x=0.2 | B�� | 5��1-x��=0.8 | C�� | x5=0.2 | D�� | ��1-x��5=0.8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | cosx-sinx | B�� | sinx-cosx | C�� | cosx+sinx | D�� | -cosx-sinx |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x-y+2=0 | B�� | 2 x+y+2=0 | C�� | x-2y+1=0 | D�� | x+2y-1=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y={��\sqrt{x}��^2}$ | B�� | $y=\sqrt{x^2}$ | C�� | $y=\left\{\begin{array}{l}x����x��0��\\-x����x��0��\end{array}\right.$ | D�� | $y=\frac{x^2}{x}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com