
【题目】为了让学生更多的了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,统计结果见下表.请你根据频率分布表解答下列问题:
序号 | 分组(分数) | 组中值 | 频数(人数) | 频率 |
1 |
| 65 | ① | 0.12 |
2 |
| 75 | 20 | ② |
3 |
| 85 | ③ | 0.24 |
4 |
| 95 | ④ | ⑤ |
合计 | 50 | 1 |
(1)填充频率分布表中的空格;
(2)规定成绩不低于85分的同学能获奖,请估计在参加的800名学生中大概有多少名同学获奖?
(3)在上述统计数据的分析中有一项计算见算法流程图,求输出的![]() 的值.
的值.

科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,根据经验,其次品率![]() 与日产量
与日产量![]() (万件)之间满足关系,
(万件)之间满足关系, (其中
(其中![]() 为常数,且
为常数,且![]() ,已知每生产1万件合格的产品以盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如
,已知每生产1万件合格的产品以盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如![]() 表示每生产10件产品,有1件次品,其余为合格品).
表示每生产10件产品,有1件次品,其余为合格品).
(1)试将生产这种产品每天的盈利额![]() (万元)表示为日产量
(万元)表示为日产量![]() (万件)的函数;
(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() .
.
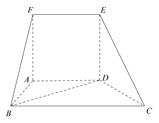
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家鞋帽商场销售同一批品牌运动鞋,每双标价为800元,甲、乙两商场销售方式如下:在甲商场买一双售价为780元,买两双每双售价为760元,依次类排,每多买一双则所买各双售价都再减少20元,但每双售价不能低于440元;乙商场一律按标价的75%销售.
(1)分别写出在甲、乙两商场购买![]() 双运动鞋所需费用的函数解析式
双运动鞋所需费用的函数解析式![]() 和
和![]() ;
;
(2)某单位需购买一批此类品牌运动鞋作为员工福利,问:去哪家商场购买花费较少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面A1B1C1,AA1=1,底面三角形A1B1C1是边长为2的正三角形,E是BC中点,则下列说法正确的是( )

①CC1与AB1所成角的余弦值为![]()
②AB⊥平面ACC1A1
③三角形AB1E为直角三角形
④A1C1∥平面AB1E
A.①②B.③④C.①③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棱长为1的正方体![]() 中,点
中,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上运动(不包括线段端点),且
上运动(不包括线段端点),且![]() .以下结论:①
.以下结论:①![]() ;②若点
;②若点![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,则由线
的中点,则由线![]() 与
与![]() 确定的平面在正方体
确定的平面在正方体![]() 上的截面为等边三角形;③四面体
上的截面为等边三角形;③四面体![]() 的体积的最大值为
的体积的最大值为![]() ;④直线
;④直线![]() 与直线
与直线![]() 的夹角为定值.其中正确的结论为______.(填序号)
的夹角为定值.其中正确的结论为______.(填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com