
【题目】如图,多面体![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 是梯形,
是梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() 且
且![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
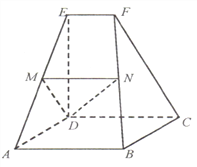
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 和平面
和平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() 的点,
的点, ![]() 垂直于圆
垂直于圆![]() 所在的平面,且
所在的平面,且![]() .
.
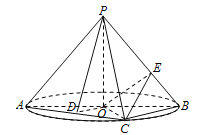
(1)若![]() 为线段
为线段![]() 的中点,求证
的中点,求证![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 体积的最大值;
体积的最大值;
(3)若![]() ,点
,点![]() 在线段
在线段![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中欧班列是推进与“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设.目前车站准备在某仓库外,利用其一侧原有墙体,建造一间墙高为3米,底面为12平方米,且背面靠墙的长方体形状的保管员室.由于此保管员室的后背靠墙,无需建造费用,因此甲工程队给出的报价为:屋子前面新建墙体的报价为每平方米400元,左右两面新建墙体报价为每平方米150元,屋顶和地面以及其他报价共计7200元.设屋子的左右两侧墙的长度均为![]() 米
米![]() .
.
(1)当左右两面墙的长度为多少时,甲工程队报价最低?
(2)现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为![]() 元
元![]() ,若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,试求
,若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com