
【题目】数列![]() :
:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,对于给定的
,…,对于给定的![]() (
(![]() ,
,![]() ),记满足不等式:
),记满足不等式:![]() (
(![]() ,
,![]() )的
)的![]() 构成的集合为
构成的集合为![]() .
.
(Ⅰ)若数列![]() ,写出集合
,写出集合![]() ;
;
(Ⅱ)如果![]() (
(![]() ,
,![]() )均为相同的单元素集合,求证:数列
)均为相同的单元素集合,求证:数列![]() ,
,![]() ,…,
,…,![]() ,…为等差数列;
,…为等差数列;
(Ⅲ)如果![]() (
(![]() ,
,![]() )为单元素集合,那么数列
)为单元素集合,那么数列![]() ,
,![]() ,…,
,…,![]() ,…还是等差数列吗?如果是等差数列,请给出证明;如果不是等差数列,请给出反例.
,…还是等差数列吗?如果是等差数列,请给出证明;如果不是等差数列,请给出反例.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析;(Ⅲ)是等差数列,证明见解析.
;(Ⅱ)证明见解析;(Ⅲ)是等差数列,证明见解析.
【解析】
(Ⅰ)由题意得,![]() ,分
,分![]() 和
和![]() 两类讨论解出不等式,再根据
两类讨论解出不等式,再根据![]() 的定义即可求出;
的定义即可求出;
(Ⅱ)由题意,若![]() 中均只有同一个元素,不妨设为
中均只有同一个元素,不妨设为![]() ,当
,当![]() 时,由题意可得
时,由题意可得![]() ,当
,当![]() 时,有
时,有![]() ,则
,则![]() 成立,从而得出证明;
成立,从而得出证明;
(Ⅲ)不妨设![]() ,
,![]() ,
,![]() ,
,![]() ,由题意可得
,由题意可得![]() ,
,![]() ,则
,则![]() ,则
,则![]() ;设
;设![]() ,则
,则![]() ,则
,则![]() ,首先证
,首先证![]() 时的情况,不妨设
时的情况,不妨设![]() ,由
,由![]() ,
,![]() 为单元素集,则
为单元素集,则![]() ;再证
;再证![]() ,由
,由![]() 和
和![]() 的定义可证
的定义可证![]() ,则
,则![]() ,则存在正整数
,则存在正整数![]() 使得
使得![]() ,而
,而![]() ,得出矛盾,从而
,得出矛盾,从而![]() ,同理可证
,同理可证![]() ,由此可得结论.
,由此可得结论.
(Ⅰ)解:由题意得,![]() 为满足不等式
为满足不等式![]() 的
的![]() 构成的集合,
构成的集合,
∵数列![]() ,
,
∴![]() ,即
,即![]() ,
,
当![]() 时,上式可化为
时,上式可化为![]() ,
,
当![]() 时,上式可化为
时,上式可化为![]() ,得
,得![]() ,
,
∴![]() ;
;
(Ⅱ)证:对于数列![]() :
:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,
,…,
若![]() 中均只有同一个元素,不妨设为
中均只有同一个元素,不妨设为![]() ,
,
下面证明数列![]() 为等差数列,
为等差数列,
当![]() 时,有
时,有![]() ,①
,①
当![]() 时,有
时,有![]() ,②
,②
∵①②两式对任意大于1的整数均成立,
∴![]() 成立,
成立,
∴数列![]() ,
,![]() ,…,
,…,![]() ,…为等差数列;
,…为等差数列;
(Ⅲ)解:对于数列![]() :
:![]() ,
,![]() ,…,
,…,![]() ,…,
,…,
不妨设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() ,知
,知![]() ,
,
由![]() ,知:
,知:![]() ,即
,即![]() ,
,
∴![]() ,∴
,∴![]() ;
;
设![]() ,则
,则![]() ,
,
这说明![]() ,则
,则![]() ,
,
∵对于数列![]() ,
,![]() 中均只有一个元素,
中均只有一个元素,
首先证![]() 时的情况,不妨设
时的情况,不妨设![]() ,
,
∵![]() ,又
,又![]() 为单元素集,∴
为单元素集,∴![]() ,
,
再证![]() ,证明如下:
,证明如下:
由![]() 的定义可知:
的定义可知:![]() ,
,![]() ,∴
,∴![]() ,
,
由![]() 的定义可知
的定义可知![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
则存在正整数![]() ,使得
,使得![]() ,③
,③
∵![]() ,
,
∴![]() ,这与③矛盾,
,这与③矛盾,
∴![]() ,
,
同理可证![]() ,即
,即![]() ,
,
∴数列![]() ,
,![]() ,…,
,…,![]() ,…还是等差数列.
,…还是等差数列.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点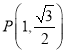 ,设它的左、右焦点分别为
,设它的左、右焦点分别为![]() 、
、![]() ,左顶点为
,左顶点为![]() ,上顶点为
,上顶点为![]() ,且满足
,且满足![]() .
.
(Ⅰ)求椭圆![]() 的标准方程和离心率;
的标准方程和离心率;
(Ⅱ)过点![]() 作不与
作不与![]() 轴垂直的直线交椭圆
轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() (异于点
(异于点![]() )两点,试判断
)两点,试判断![]() 的大小是否为定值,并说明理由.
的大小是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某校某班44名同学的某次考试的物理成绩y和数学成绩x的散点图:
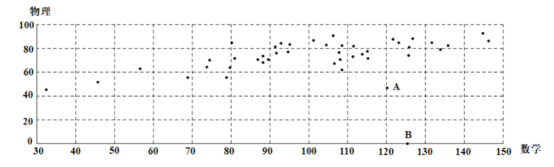
根据散点图可以看出y与x之间有线性相关关系,但图中有两个异常点A,B.经调查得知,A考生由于重感冒导致物理考试发挥失常,B生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计量的值:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 分别表示这42名同学的数学成绩、物理成绩,
分别表示这42名同学的数学成绩、物理成绩,![]() .y与x的相关系数
.y与x的相关系数![]() .
.
(1)若不剔除A、B两名考生的数据,用44数据作回归分析,设此时y与x的相关系数为![]() ,试判断
,试判断![]() 与r的大小关系,并说明理由;
与r的大小关系,并说明理由;
(2)求y关于x的线性回归方程(系数精确到![]() ),并估计如果B考生参加了这次物理考试(已知B考生的数学成绩为125分),物理成绩是多少?(精确到个位).
),并估计如果B考生参加了这次物理考试(已知B考生的数学成绩为125分),物理成绩是多少?(精确到个位).
附:回归方程![]() 中,
中, .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数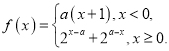 给出下列四个结论:①对
给出下列四个结论:①对![]() ,
,![]() ,使得
,使得![]() 无解;②对
无解;②对![]() ,
,![]() ,使得
,使得![]() 有两解;③当
有两解;③当![]() 时,
时,![]() ,使得
,使得![]() 有解;④当
有解;④当![]() 时,
时,![]() ,使得
,使得![]() 有三解.其中,所有正确结论的序号是______.
有三解.其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
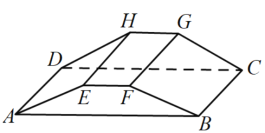
【题目】我国古代《九章算术》中将上,下两面为平行矩形的六面体称为刍童.如图的刍童![]() 有外接球,且
有外接球,且![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 与平面
与平面![]() 间的距离为
间的距离为![]() ,则该刍童外接球的体积为( )
,则该刍童外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
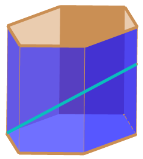
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六、八是中国人的吉利数字,所以好多瓷器都做成六棱形和八棱形.数学李老师有一个正六棱柱形状的笔筒,如图,底面边长为![]() ,高为
,高为![]() (底部及筒壁厚度忽略不计).一根长度为
(底部及筒壁厚度忽略不计).一根长度为![]() 的圆铁棒
的圆铁棒![]() (粗细忽略不计)斜放在笔筒内部,
(粗细忽略不计)斜放在笔筒内部,![]() 的一端置于正六棱柱某一侧棱的底端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为______
的一端置于正六棱柱某一侧棱的底端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
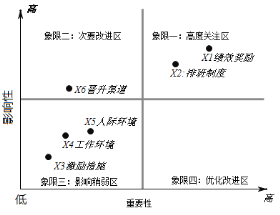
【题目】2020年1月,某公司以问卷的形式调查影响员工积极性的六项关键指标:绩效奖励、排班制度、激励措施、工作环境、人际关系、晋升渠道,在确定各项指标权重结果后,进而得到指标重要性分析象限图(如图).若客户服务中心从中任意抽取不同的两项进行分析,则这两项来自影响稍弱区的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com