
【题目】我国全面二孩政策已于2016年1月1日起正式实施.国家统计局发布的数据显示,从2012年到2017年,中国的人口自然增长率变化始终不大,在5‰上下波动(如图).

为了了解年龄介于24岁至50岁之间的适孕夫妻对生育二孩的态度如何,统计部门按年龄分为9组,每组选取150对夫妻进行调查统计有生育二孩意愿的夫妻数,得到下表:
年龄区间 |
|
|
|
|
|
|
|
|
|
有意愿数 | 80 | 81 | 87 | 86 | 84 | 83 | 83 | 70 | 66 |
(1)设每个年龄区间的中间值为![]() ,有意愿数为
,有意愿数为![]() ,求样本数据的线性回归直线方程,并求该模型的相关系数
,求样本数据的线性回归直线方程,并求该模型的相关系数![]() (结果保留两位小数);
(结果保留两位小数);
(2)从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
(参考数据和公式: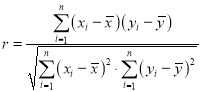 ,
,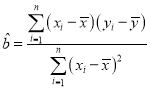 ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)![]() .-0.63(2)
.-0.63(2)![]()
【解析】
(1)根据题意,结合参考数据和公式,代值计算即可求得结果;
(2)列举出所有选取的结果,找出满足题意的选取结果,根据古典概型的概率计算公式即可求得.
解:(1)由题意可求得:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,
![]() ,
,
∴![]() .
.
∴![]() .∴
.∴![]() .
.
∴回归直线方程为![]() .
.
∴ .
.
(2)由题意可知,在![]() ,
,![]() ,
,![]() 年龄段中,
年龄段中,
超过半数的夫要有生育二孩意愿,在![]() ,
,![]() 年龄段中,
年龄段中,
超过半数的夫妻没有生育二孩意愿.
设从![]() ,
,![]() ,
,![]() 年龄段中选出的夫妻分别为
年龄段中选出的夫妻分别为![]() ,
,![]() ,
,![]() ,
,
从![]() ,
,![]() 年龄段中选出的夫妻分别为
年龄段中选出的夫妻分别为![]() ,
,![]() .
.
则从中选出2对夫妻的所有可能结果为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10种情况.
,共10种情况.
其中恰有一对不愿意生育二孩的夫妻的情况有![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,共6种.
,共6种.
∴恰有一对不愿意生育二孩的夫妻的概率![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的方程为
的方程为![]() ,且直线
,且直线![]() 与以原点为圆心,椭圆
与以原点为圆心,椭圆![]() 短轴长为直径的圆相切.
短轴长为直径的圆相切.
(1)求![]() 的值;
的值;
(2)若椭圆![]() 左右顶点分别为
左右顶点分别为![]() ,过点
,过点![]() 作直线
作直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 位于第一象限,
位于第一象限,![]() 在线段
在线段![]() 上.
上.
①若![]() 和
和![]() 的面积分别为
的面积分别为![]() ,问是否存在这样的直线
,问是否存在这样的直线![]() 使得
使得![]() ?请说明理由;
?请说明理由;
②直线![]() 与直线
与直线![]() 交于点
交于点![]() ,连结
,连结![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现给出三个条件:①函数![]() 的图象关于直线
的图象关于直线![]() 对称;②函数
对称;②函数![]() 的图象关于点
的图象关于点![]() 对称;③函数
对称;③函数![]() 的图象上相邻两个最高点的距离为
的图象上相邻两个最高点的距离为![]() .从中选出两个条件补充在下面的问题中,并以此为依据求解问题.
.从中选出两个条件补充在下面的问题中,并以此为依据求解问题.
已知函数![]() (
(![]() ,
,![]() ),_____,_____.求函数
),_____,_____.求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn和通项an满足![]() .
.
(1)求数列{an}的通项公式;
(2)等差数列{bn}中,b1=3a1,b2=2,求数列{an+bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校运动会男生组田径综合赛以选手三项运动的综合积分高低决定排名.具体积分规则如表1所示,某代表队四名男生的模拟成绩如表2.
表1 田径综合赛项目及积分规则
项目 | 积分规则 |
| 以 |
跳高 | 以 |
掷实心球 | 以 |
表2 某队模拟成绩明细
姓名 | 100米跑(秒) | 跳高(米) | 掷实心球(米) |
甲 |
|
|
|
乙 |
|
|
|
丙 |
|
|
|
丁 |
|
|
|
根据模拟成绩,该代表队应选派参赛的队员是:( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面ABCD⊥平面PAD,AD∥BC,AB=BC![]() AD=1,∠APD=∠BAD=90°.
AD=1,∠APD=∠BAD=90°.
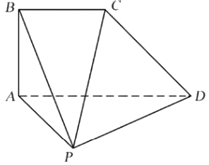
(1)求证:PD⊥PB;
(2)当PA=PD时,求三棱锥P﹣BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,曲线C的参数方程为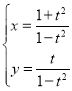 (t为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(
(t为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(![]() )
)![]() .
.
(1)求曲线C和直线l的直角坐标方程;
(2)若直线l交曲线C于A,B两点,交x轴于点P,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com