
 中,角
中,角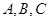 的对边分别为
的对边分别为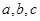 ,已知
,已知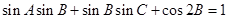 .
.
(1)求证: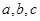 成等差数列;
成等差数列;
(2)若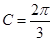
 ,求
,求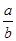 的值.
的值.
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计, 可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=a·b,其中向量
 ,向量
,向量
 .
.
(1)求f(x)的最小正周期;
(2)在∆ABC中,a,b,c分别是角A,B,C的对边,f(A)=2,a= ,b+c=3,求b,c的长.
,b+c=3,求b,c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
火车站 北偏东
北偏东 方向的
方向的 处有一电视塔,火车站正东方向的
处有一电视塔,火车站正东方向的 处有一小汽车,测得
处有一小汽车,测得 距离为31
距离为31 ,该小汽车从
,该小汽车从 处以60公里每小时的速度前往火车站,20分钟后到达
处以60公里每小时的速度前往火车站,20分钟后到达 处,测得离电视塔21
处,测得离电视塔21 ,问小汽车到火车站还需多长时间?
,问小汽车到火车站还需多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某人沿一条折线段组成的小路前进,从 到
到 ,方位角(从正北方向顺时针转到
,方位角(从正北方向顺时针转到 方向所成的角)是
方向所成的角)是 ,距离是3km;从
,距离是3km;从 到
到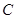 ,方位角是110°,距离是3km;从
,方位角是110°,距离是3km;从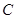 到
到 ,方位角是140°,距离是(
,方位角是140°,距离是( )km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
)km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com