解:(1)∵圆C
1与直线
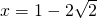
相切于点
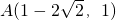
,
∴圆心C
1在直线y=1上,…(1分)
又圆心C
1在直线x-y=0上,
∴圆心C
1为直线y=1和直线x-y=0的交点,即点(1,1).…(2分)
∵圆C
1与直线
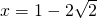
相切,
∴圆C
1的半径等于点(1,1)到直线
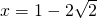
的距离,
即圆C
1的半径为
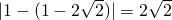
∴圆C
1的方程为(x-1)
2+(y-1)
2=8…(5分)
(2)∵圆心C
1到直线l
2的距离为
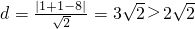
…(7分)
∴直线l
2与圆C
1相离.…(8分)
(3)由已知,可设圆C
2的方程为(x-a)
2+(y-b)
2=8,
∵圆C
2经过点(1,1),
∴(1-a)
2+(1-b)
2=8,即(a-1)
2+(b-1)
2=8,
∴圆C
2的圆心C
2(a,b)在圆C
1上.…(10分)
设直线l
2:x+y-8=0与圆C
2的交点分别为M,N,MN的中点为P,
由圆的性质可得:
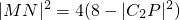
,
所以求直线l
2被圆C
2截得弦长MN的最大值即求C
2P的最小值.…(12分)
又因为C
1到直线l
2的距离为
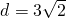
,
所以C
2P的最小值为
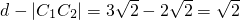
,
所以
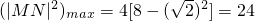
,
即

,
故直线l
2被圆C
2截得弦长的最大值为

.…(14分)
分析:(1)根据圆C
1与直线
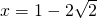
相切于点
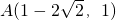
,可得圆心C
1在直线y=1上,利用圆心C
1在直线x-y=0上,可求圆心C
1的坐标,利用圆C
1与直线
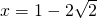
相切,可求圆C
1的半径,从而可得圆C
1的方程;
(2)利用圆心C
1到直线l
2的距离与半径的关系,可得直线l
2与圆C
1的位置关系;
(3)先确定圆C
2的圆心C
2(a,b)在圆C
1上,设直线l
2:x+y-8=0与圆C
2的交点分别为M,N,MN的中点为P,进而可知求直线l
2被圆C
2截得弦长MN的最大值即求C
2P的最小值,利用C
2P的最小值为d-|C
1C
2|,可求直线l
2被圆C
2截得弦长的最大值.
点评:本题以直线与圆相切为载体,考查圆的标准方程,考查直线与圆的位置关系,考查圆中的弦长问题,熟练运用圆心到直线的距离是解题的关键,综合性强.

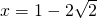 相切于点A(
相切于点A(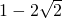 ,1),直线l2:x+y-8=0.
,1),直线l2:x+y-8=0. 的动圆C2经过点(1,1),当圆C2与直线l2相交时,求直线l2被圆C2截得弦长的最大值.
的动圆C2经过点(1,1),当圆C2与直线l2相交时,求直线l2被圆C2截得弦长的最大值.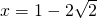 相切于点
相切于点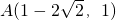 ,
,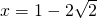 相切,
相切,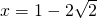 的距离,
的距离,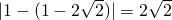
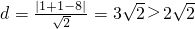 …(7分)
…(7分)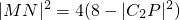 ,
,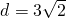 ,
,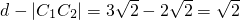 ,
,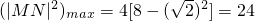 ,
, ,
, .…(14分)
.…(14分)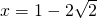 相切于点
相切于点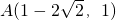 ,可得圆心C1在直线y=1上,利用圆心C1在直线x-y=0上,可求圆心C1的坐标,利用圆C1与直线
,可得圆心C1在直线y=1上,利用圆心C1在直线x-y=0上,可求圆心C1的坐标,利用圆C1与直线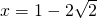 相切,可求圆C1的半径,从而可得圆C1的方程;
相切,可求圆C1的半径,从而可得圆C1的方程;

 应用题作业本系列答案
应用题作业本系列答案 相切.
相切. ,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2;
,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2; 时,得到曲线C,问是否存在与l1垂直的一条直线l与曲线C交于B、D两点,且∠BOD为钝角,请说明理由.
时,得到曲线C,问是否存在与l1垂直的一条直线l与曲线C交于B、D两点,且∠BOD为钝角,请说明理由.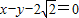 相切.
相切.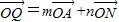 ,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2;
,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2;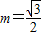 时,得到曲线C,问是否存在与l1垂直的一条直线l与曲线C交于B、D两点,且∠BOD为钝角,请说明理由.
时,得到曲线C,问是否存在与l1垂直的一条直线l与曲线C交于B、D两点,且∠BOD为钝角,请说明理由.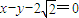 相切.
相切.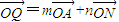 ,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2;
,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2;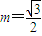 时,得到曲线C,问是否存在与l1垂直的一条直线l与曲线C交于B、D两点,且∠BOD为钝角,请说明理由.
时,得到曲线C,问是否存在与l1垂直的一条直线l与曲线C交于B、D两点,且∠BOD为钝角,请说明理由.