
【题目】已知函数![]() .
.
(1)若![]() 在定义域上不单调,求
在定义域上不单调,求![]() 的取值范围;
的取值范围;
(2)设![]() 分别是
分别是![]() 的极大值和极小值,且
的极大值和极小值,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:由已知![]() ,
,
(1)①若![]() 在定义域上单调递增,讨论可得
在定义域上单调递增,讨论可得![]() ;②若
;②若![]() 在定义域上单调递减,讨论可得
在定义域上单调递减,讨论可得![]() .据此可得
.据此可得![]() .
.
(2)由(1)知,![]() .令
.令![]() 的两根分别为
的两根分别为![]() ,设
,设![]() ,则
,则![]() ,计算可得
,计算可得![]() 令
令![]() ,换元讨论可得
,换元讨论可得![]() .
.
详解:由已知![]() ,
,
(1)①若![]() 在定义域上单调递增,则
在定义域上单调递增,则![]() ,即
,即![]() 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
而![]() ,所以
,所以![]() ;
;
②若![]() 在定义域上单调递减,则
在定义域上单调递减,则![]() ,即
,即![]() 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
而![]() ,所以
,所以![]() .
.
因为![]() 在定义域上不单调,所以
在定义域上不单调,所以![]() ,即
,即![]() .
.
(2)由(1)知,欲使![]() 在(0,+∞)有极大值和极小值,必须
在(0,+∞)有极大值和极小值,必须![]() .
.
又![]() ,所以
,所以![]() .
.
令![]() 的两根分别为
的两根分别为![]() ,
,
即![]() 的两根分别为
的两根分别为![]() ,于是
,于是![]() .
.
不妨设![]() ,
,
则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,
,
所以![]()
![]()
![]()
令![]() ,于是
,于是![]() .
.
![]() ,
,
由![]() ,得
,得![]() .
.
因为![]() ,
,
所以![]() 在
在![]() 上为减函数.
上为减函数.
所以![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】设等比数列a1,a2,a3,a4的公比为q,等差数列b1,b2,b3,b4的公差为d,且![]() .记
.记![]() (i1,2,3,4).
(i1,2,3,4).
(1)求证:数列![]() 不是等差数列;
不是等差数列;
(2)设![]() ,
, ![]() .若数列
.若数列![]() 是等比数列,求b2关于d的函数关系式及其定义域;
是等比数列,求b2关于d的函数关系式及其定义域;
(3)数列![]() 能否为等比数列?并说明理由.
能否为等比数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对![]() 两位选手,随机调查了20个学生的评分,得到下面的茎叶图:
两位选手,随机调查了20个学生的评分,得到下面的茎叶图:

所得分数 | 低于60分 | 60分到79分 | 不低于80分 |
分流方向 | 淘汰出局 | 复赛待选 | 直接晋级 |
(1)通过茎叶图比较![]() 两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
(2)举办方将会根据评分结果对选手进行三向分流,根据所得分数,估计![]() 两位选手中哪位选手直接晋级的概率更大,并说明理由.
两位选手中哪位选手直接晋级的概率更大,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程(2+λ)x-(1+λ)y-2(3+2λ)=0与点P(-2,2).
(1)证明:对任意的实数λ,该方程都表示直线,且这些直线都经过同一定点,并求出这一定点的坐标;
(2)证明:该方程表示的直线与点P的距离d小于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),
是参数),
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 任一点为
任一点为![]() ,求点
,求点![]() 直线
直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)(2017·开封二模)为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率.
(2)检验结束后,甲、乙两名运动员的成绩用茎叶图表示如图:
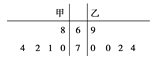
计算说明哪位运动员的成绩更稳定.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校某班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生有14人.

(1)求总人数N和分数在120~125的人数n;
(2)利用频率分布直方图,估算该班学生数学成绩的众数和中位数各是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】摩拜单车和![]() 小黄车等各种共享单车的普及给我们的生活带来了便利.已知某共享单车的收费标准是:每车使用不超过1小时(包含1小时)是免费的,超过1小时的部分每小时收费1元(不足1小时的部分按1小时计算,例如:骑行2.5小时收费2元).现有甲、乙两人各自使用该种共享单车一次.设甲、乙不超过1小时还车的概率分别为
小黄车等各种共享单车的普及给我们的生活带来了便利.已知某共享单车的收费标准是:每车使用不超过1小时(包含1小时)是免费的,超过1小时的部分每小时收费1元(不足1小时的部分按1小时计算,例如:骑行2.5小时收费2元).现有甲、乙两人各自使用该种共享单车一次.设甲、乙不超过1小时还车的概率分别为![]() 1小时以上且不超过2小时还车的概率分别为
1小时以上且不超过2小时还车的概率分别为![]() 两人用车时间都不会超过3小时.
两人用车时间都不会超过3小时.
(Ⅰ)求甲乙两人所付的车费相同的概率;
(Ⅱ)设甲乙两人所付的车费之和为随机变量![]() 求
求![]() 的分布列及数学期望
的分布列及数学期望![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com