
【题目】从柳州铁一中高二男生中随机选取100名学生,将他们的体重(单位:![]() )数据绘制成频率分布直方图,如图所示.
)数据绘制成频率分布直方图,如图所示.
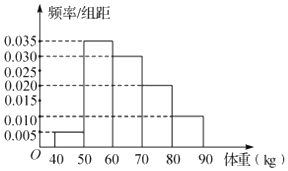
(1)估计该校的100名同学体重的平均值和方差(同一组数据用该组区间的中点值代表);
(2)若要从体重在![]() 内的两组男生中,用分层抽样的方法选取5人,再从这5人中随机抽取2人,求被抽取的两位同学来自不同组的概率.
内的两组男生中,用分层抽样的方法选取5人,再从这5人中随机抽取2人,求被抽取的两位同学来自不同组的概率.
【答案】(1)平均值64.5,方差114.75; (2)![]()
【解析】
(1)由频率分布直方图先求得各组的频率,即可由频率分布直方图中各小矩形底边中点乘以频率求和,得平均数;由方差公式,可计算数据的方差.
(2)由题意线求得体重在![]() 及
及![]() 的男生人数,利用分层抽样比可得在各组内抽取人数.由古典概型概率求法,随机抽取2人的所有情况,即可得解.
的男生人数,利用分层抽样比可得在各组内抽取人数.由古典概型概率求法,随机抽取2人的所有情况,即可得解.
(1)依频率分布直方图得各组的频率依次为:
0.05,0.35,0.30,0.20,0.10;
计算这100名学生的平均体重约为:
![]() ;
;
方差为:![]()
![]() .
.
(2)由(1)及已知可得:体重在![]() 及
及![]() 的男生分别为:
的男生分别为:
![]() (人),
(人),![]() (人),
(人),
从中用分层抽样的方法选5人,则体重在![]() 内的应选3人,记为a,b,c;
内的应选3人,记为a,b,c;
体重在![]() 内的应选2人;记为1,2;
内的应选2人;记为1,2;
随机抽取2名同学有如下种情形:![]() ,
,![]() 共有10个基本事件;
共有10个基本事件;
其中符合“抽取的2名同学来自不同组”的基本事件有6个,
所以抽取的2名同学来自不同组的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.在回归分析中,相关指数![]() 越大,说明残差平方和越小,回归效果越好
越大,说明残差平方和越小,回归效果越好
B.线性回归方程对应的直线![]() 至少经过其样本数据点中的一个点
至少经过其样本数据点中的一个点
C.在线性回归分析中,相关系数为![]() ,
,![]() 越接近于1,相关程度越大
越接近于1,相关程度越大
D.在回归直线![]() 中,变量
中,变量![]() 每增加一个单位,变量
每增加一个单位,变量![]() 大约增加0.5个单位
大约增加0.5个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
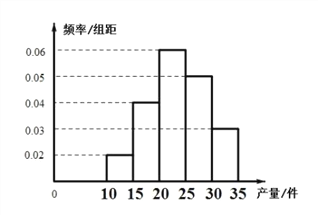
【题目】为了考查某厂2000名工人的生产技能情况,随机抽查了该厂![]() 名工人某天的产量(单位:件),整理后得到如下的频率分布直方图(产量的区间分别为:
名工人某天的产量(单位:件),整理后得到如下的频率分布直方图(产量的区间分别为:![]() ),其中产量在
),其中产量在![]() 的工人有6名.
的工人有6名.
(1)求这一天产量不小于25的工人数;
(2)该厂规定从产量低于20件的工人中选取2名工人进行培训,求这两名工人不在同一分组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凤鸣山中学的高中女生体重![]() (单位:kg)与身高
(单位:kg)与身高![]() (单位:cm)具有线性相关关系,根据一组样本数据
(单位:cm)具有线性相关关系,根据一组样本数据![]() (
(![]() ),用最小二乘法近似得到回归直线方程为
),用最小二乘法近似得到回归直线方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.![]() 与
与![]() 具有正线性相关关系
具有正线性相关关系
B.回归直线过样本的中心点![]()
C.若该中学某高中女生身高增加1cm,则其体重约增加0.85kg
D.若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有两家共享单车公司,在市场上分别投放了黄、蓝两种颜色的单车,已知黄、蓝两种颜色的单车的投放比例为2:1.监管部门为了了解两种颜色的单车的质量,决定从市场中随机抽取5辆单车进行体验,若每辆单车被抽取的可能性相同.
(1)求抽取的5辆单车中有2辆是蓝色颜色单车的概率;
(2)在骑行体验过程中,发现蓝色单车存在一定质量问题,监管部门决定从市场中随机地抽取一辆送技术部门作进一步抽样检测,并规定若抽到的是蓝色单车,则抽样结束,若抽取的是黄色单车,则将其放回市场中,并继续从市场中随机地抽取下一辆单车,并规定抽样的次数最多不超过![]() (
(![]() )次.在抽样结束时,已取到的黄色单车以
)次.在抽样结束时,已取到的黄色单车以![]() 表示,求
表示,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 是异面直线,给出下列结论:
是异面直线,给出下列结论:
①一定存在平面![]() ,使直线
,使直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ;
;
②一定存在平面![]() ,使直线
,使直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ;
;
③一定存在无数个平面![]() ,使直线
,使直线![]() 与平面
与平面![]() 交于一个定点,且直线
交于一个定点,且直线![]() 平面
平面![]() .
.
则所有正确结论的序号为( )
A.①②B.②C.②③D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
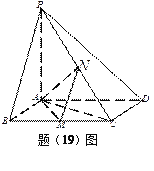
如图,已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
, ![]() 分别是
分别是![]() 的中点。
的中点。
(1)证明: ![]() ;
;
(2)若![]() 为
为![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成最大角
所成最大角
的正切值为![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com