
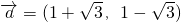 ,
,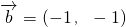 ,求
,求 与
与 所成角的大小,
所成角的大小, 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源:2010年北京市首师大附中高三大练习数学试卷10(文科)(解析版) 题型:解答题
 .证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求该圆的方程;
.证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求该圆的方程; .设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值.
.设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值.查看答案和解析>>
科目:高中数学 来源:2011年高三数学第一轮复习精练:直线和圆(解析版) 题型:解答题
 .证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求该圆的方程;
.证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求该圆的方程; .设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值.
.设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com