
A.k∈R B.k<![]()
C.![]() <k<0 D.
<k<0 D.![]() <k<
<k<![]()
思路解析:利用圆的几何性质,过点P作C的切线有两条,则表明点P在圆C外,即两点之间的距离大于半径.这里不需要将圆的一般方程化为标准方程.
设圆C的标准方程为(x-a)2+(y-b)2=r2,
则应该有(x-a)2+(y-b)2-r2=x2+y2+kx+2y+k2,
因任意一点A(x,y)在圆C外的条件是(x-a)2+(y-b)2>r2,
根据前一等式有x2+y2+kx+2y+k2>0,
于是有结论:只要将P点坐标代入圆的方程左端x2+y2+kx+2y+k2使得其大于0,
就有P在圆外.将P(1,2)坐标代入后得到k2+k+9>0,
因k2+k+9=(k+![]() )2+
)2+![]() >0,
>0,
所以此式对任意k都成立,
所以k的取值范围是全体实数.
答案:A


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求双曲线的方程;
(2)过点F的直线l,交双曲线于A、B两点,若弦长|AB|不超过4,求l的倾斜角范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
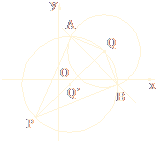
已知点P(-2,-3)和以Q为圆心的圆(x-4)2+(y-2)2=9.
(1)画出以PQ为直径,Q′为圆心的圆,再求出它的方程.
(2)作出以Q为圆心的圆和以Q′为圆心的圆的两个交点A、B.直线PA、PB是以Q为圆心的圆的切线吗?为什么?
(3)求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西师大附中,临川一中高三期末联考理科数学试卷(解析版) 题型:选择题
已知点P(3,4)和圆C:(x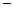 2)2+y2=4,A,B是圆C上两个动点,且|AB|=
2)2+y2=4,A,B是圆C上两个动点,且|AB|=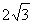 ,则
,则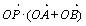 (O为坐标原点)的取值范围是( )
(O为坐标原点)的取值范围是( )
A.[3,9] B.[1,11] C.[6,18] D.[2,22]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com