
【题目】若函数![]() 同时满足:(1)对于定义域上的任意
同时满足:(1)对于定义域上的任意![]() ,恒有
,恒有![]() ;(2)对于定义域上的任意
;(2)对于定义域上的任意![]() ,
,![]() ,当
,当![]() 时,恒有,
时,恒有,![]() 则称函数
则称函数![]() 为“理想函数”.给出下列四个函数中:①
为“理想函数”.给出下列四个函数中:①![]() ; ②
; ②![]() ; ③
; ③![]() ;④
;④ ,则被称为“理想数”的有________(填相应的序号).
,则被称为“理想数”的有________(填相应的序号).
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知以坐标原点![]() 为圆心的圆与抛物线
为圆心的圆与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,与抛物线
,与抛物线![]() 的准线相交于不同的两点
的准线相交于不同的两点![]() ,
, ![]() ,且
,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若不经过坐标原点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,且满足
,且满足![]() .证明直线
.证明直线![]() 过定点
过定点![]() ,并求出点
,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,PA=2,∠ABC=90°,![]() ,BC=1,
,BC=1, ![]() ,∠ACD=60°,E为CD的中点.
,∠ACD=60°,E为CD的中点.

(1)求证:BC∥平面PAE;
(2)求点A到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蛋糕店制作并销售一款蛋糕,当天每售出![]() 个获得利润
个获得利润![]() 元,未售出的每个亏损
元,未售出的每个亏损![]() 元.根据以往
元.根据以往![]() 天的资料统计,得到如下需求量表.元日这天,此蛋糕店制作了这款蛋糕
天的资料统计,得到如下需求量表.元日这天,此蛋糕店制作了这款蛋糕![]() 个.以
个.以![]() (单位:个,
(单位:个, ![]() )表示这天的市场需求量.
)表示这天的市场需求量. ![]() (单位:元)表示这天出售这款蛋糕获得的利润.
(单位:元)表示这天出售这款蛋糕获得的利润.
需求量/个 |
|
|
|
|
|
天数 | 15 | 25 | 30 | 20 | 10 |
(1)当![]() 时,若
时,若![]() 时获得的利润为
时获得的利润为![]() ,
, ![]() 时获得的利润为
时获得的利润为![]() ,试比较
,试比较![]() 和
和![]() 的大小;
的大小;
(2)当![]() 时,根据上表,从利润
时,根据上表,从利润![]() 不少于
不少于![]() 元的天数中,按需求量分层抽样抽取
元的天数中,按需求量分层抽样抽取![]() 天,
天,
(ⅰ)求这![]() 天中利润为
天中利润为![]() 元的天数;
元的天数;
(ⅱ)再从这![]() 天中抽取
天中抽取![]() 天做进一步分析,设这
天做进一步分析,设这![]() 天中利润为
天中利润为![]() 元的天数为
元的天数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题α:函数![]() 的定义域是R;命题β:在R上定义运算:xy=x(1-y).不等式(x-a)(x+a)<1对任意实数x都成立.
的定义域是R;命题β:在R上定义运算:xy=x(1-y).不等式(x-a)(x+a)<1对任意实数x都成立.
(1)若α、β中有且只有一个真命题,求实数a的取值范围;
(2)若α、β中至少有一个真命题,求实数a的取值范围;
(3)若α、β中至多有一个真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中非毕业班学生人数分布情况如下表,为了了解这2000个学生的体重情况,从中随机抽取160个学生并测量其体重数据,根据测量数据制作了下图所示的频率分布直方图.
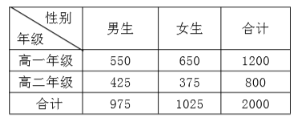

(1)为了使抽取的160个样品更具代表性,宜采取分层抽样,请你给出一个你认为合适的分层抽样方案,并确定每层应抽取的样品个数;
(2)根据频率分布直方图,求![]() 的值,并估计全体非毕业班学生中体重在
的值,并估计全体非毕业班学生中体重在![]() 内的人数;
内的人数;
(3)已知高一全体学生的平均体重为![]() ,高二全体学生的平均体重为
,高二全体学生的平均体重为![]() ,试估计全体非毕业班学生的平均体重.
,试估计全体非毕业班学生的平均体重.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若f (x)在区间(-∞,2)上为单调递增函数,求实数a的取值范围;
(2)若a=0,x0<1,设直线y=g(x)为函数f (x)的图象在x=x0处的切线,求证:f (x)≤g(x).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com