
ЁОЬтФПЁПШєдВ![]() ЃЈ
ЃЈ![]() ЃЉЩЯНіга
ЃЉЩЯНіга![]() ИіЕуЕНжБЯп
ИіЕуЕНжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЌдђЪЕЪ§
ЃЌдђЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ЁОД№АИЁПB
ЁОНтЮіЁПдВаФЕНжБЯп![]() ОрРыЮЊ
ОрРыЮЊ![]() ЃЌЫљвдвЊга
ЃЌЫљвдвЊга![]() ИіЕуЕНжБЯп
ИіЕуЕНжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЌаш
ЃЌаш![]() ЃЌбЁB.
ЃЌбЁB.
ЕуОІЃКгыдВгаЙиЕФГЄЖШЛђОрРыЕФзюжЕЮЪЬтЕФНтЗЈЃЎвЛАуИљОнГЄЖШЛђОрРыЕФМИКЮвтвхЃЌРћгУдВЕФМИКЮаджЪЪ§аЮНсКЯЧѓНтЃЎ
ЁОЬтаЭЁПЕЅбЁЬт
ЁОНсЪјЁП
15
ЁОЬтФПЁПЩш![]() КЭ
КЭ![]() ЮЊЫЋЧњЯп
ЮЊЫЋЧњЯп![]() ЕФСНИіНЙЕуЃЌШє
ЕФСНИіНЙЕуЃЌШє![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЪЧе§Ш§НЧаЮЕФШ§ИіЖЅЕуЃЌдђЫЋЧњЯпЕФНЅНќЯпЗНГЬЪЧЃЈ ЃЉ
ЪЧе§Ш§НЧаЮЕФШ§ИіЖЅЕуЃЌдђЫЋЧњЯпЕФНЅНќЯпЗНГЬЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 ЛЦИдЬьЬьСЗПкЫуЬтПЈЯЕСаД№АИ
ЛЦИдЬьЬьСЗПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫФРтзЖ![]() жаЃЌЦНУц
жаЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌВрУц
ЃЌВрУц![]() ЪЧБпГЄЮЊ
ЪЧБпГЄЮЊ![]() ЕФЕШБпШ§НЧаЮЃЌЕзУц
ЕФЕШБпШ§НЧаЮЃЌЕзУц![]() ЪЧОиаЮЃЌЧв
ЪЧОиаЮЃЌЧв![]() ЃЌдђИУЫФРтзЖЭтНгЧђЕФБэУцЛ§ЕШгк__________.
ЃЌдђИУЫФРтзЖЭтНгЧђЕФБэУцЛ§ЕШгк__________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШ§РтзЖ![]() жаЃЌВрУц
жаЃЌВрУц![]() ДЙжБЕзУцЃЌ
ДЙжБЕзУцЃЌ ![]() ЪЧЕзУцзюГЄЕФБпЃЛЭМ1ЪЧШ§РтзЖ
ЪЧЕзУцзюГЄЕФБпЃЛЭМ1ЪЧШ§РтзЖ![]() ЕФШ§ЪгЭМЃЌЦфжаЕФВрЪгЭМКЭИЉЪгЭМОљЮЊжБНЧШ§НЧаЮЃЛЭМ2ЪЧгУаБЖўВтЛЗЈЛГіЕФШ§РтзЖ
ЕФШ§ЪгЭМЃЌЦфжаЕФВрЪгЭМКЭИЉЪгЭМОљЮЊжБНЧШ§НЧаЮЃЛЭМ2ЪЧгУаБЖўВтЛЗЈЛГіЕФШ§РтзЖ![]() ЕФжБЙлЭМЕФвЛВПЗжЃЌЦфжаЕу
ЕФжБЙлЭМЕФвЛВПЗжЃЌЦфжаЕу![]() дк
дк![]() ЦНУцФкЃЎ
ЦНУцФкЃЎ
ЃЈЂёЃЉЧыдкЭМ2жаНЋШ§РтзЖ![]() ЕФжБЙлЭМВЙГфЭъећЃЌВЂжИГіШ§РтзЖ
ЕФжБЙлЭМВЙГфЭъећЃЌВЂжИГіШ§РтзЖ![]() ЕФФФаЉУцЪЧжБНЧШ§НЧаЮЃЛ
ЕФФФаЉУцЪЧжБНЧШ§НЧаЮЃЛ![]()
![]()
ЃЈЂђЃЉЩшЖўУцНЧ![]() ЕФДѓаЁЮЊ
ЕФДѓаЁЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈЂѓЃЉЧѓЕу![]() ЕНУц
ЕНУц![]() ЕФОрРыЃЎ
ЕФОрРыЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊгыЧњЯп![]() ЯрЧаЕФжБЯп
ЯрЧаЕФжБЯп![]() ЃЌгы
ЃЌгы![]() жсЃЌ
жсЃЌ ![]() жсНЛгк
жсНЛгк![]() СНЕуЃЌ
СНЕуЃЌ ![]() ЮЊдЕуЃЌ
ЮЊдЕуЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЃЈ
ЃЌЃЈ ![]() ЃЉ.
ЃЉ.
ЃЈ1ЃЉЧѓжЄ:ЃК ![]() гы
гы![]() ЯрЧаЕФЬѕМўЪЧЃК
ЯрЧаЕФЬѕМўЪЧЃК ![]() .
.
ЃЈ2ЃЉЧѓЯпЖЮ![]() жаЕуЕФЙьМЃЗНГЬЃЛ
жаЕуЕФЙьМЃЗНГЬЃЛ
ЃЈ3ЃЉЧѓШ§НЧаЮ![]() УцЛ§ЕФзюаЁжЕ.
УцЛ§ЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌжБШ§Ртжљ![]() жаЃЌ
жаЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЮЊРт
ЮЊРт![]() ЕФжаЕу.
ЕФжаЕу.
ЃЈЂёЃЉЬНОПжБЯп![]() гыЦНУц
гыЦНУц![]() ЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈЂђЃЉШє![]() ЃЌЧѓШ§РтзЖ
ЃЌЧѓШ§РтзЖ![]() ЕФЬхЛ§.
ЕФЬхЛ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕxoyжаЃЌЦфжаA(0,0),B(2,0),C(1,1),D(0,1),ЭМжадВЛЁЫљдкдВЕФдВаФЮЊЕуCЃЌАыОЖЮЊ![]() ЃЌЧвЕуPдкЭМжавѕгАВПЗжЃЈАќРЈБпНчЃЉдЫЖЏ.Шє
ЃЌЧвЕуPдкЭМжавѕгАВПЗжЃЈАќРЈБпНчЃЉдЫЖЏ.Шє![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌдђ
ЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
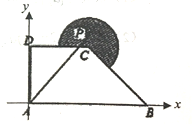
A. [2,3+![]() ] B. [2,3+
] B. [2,3+![]() ] C. [3-
] C. [3-![]() , 3+
, 3+![]() ] D. [3-
] D. [3-![]() , 3+
, 3+![]() ]
]
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§f(x)дкRЩЯПЩЕМЃЌЦфЕМКЏЪ§ЮЊfЁф(x)ЃЌЧвКЏЪ§yЃН(1Ѓx)fЁф(x)ЕФЭМЯёШчЭМЫљЪОЃЌдђЯТСаНсТлжавЛЖЈГЩСЂЕФЪЧ(ЁЁЁЁ)
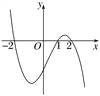
A. КЏЪ§f(x)гаМЋДѓжЕf(2)КЭМЋаЁжЕf(1) B. КЏЪ§f(x)гаМЋДѓжЕf(Ѓ2)КЭМЋаЁжЕf(1)
C. КЏЪ§f(x)гаМЋДѓжЕf(2)КЭМЋаЁжЕf(Ѓ2) D. КЏЪ§f(x)гаМЋДѓжЕf(Ѓ2)КЭМЋаЁжЕf(2)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЃК
ЃК ![]() ЕФНЙЕуЮЊ
ЕФНЙЕуЮЊ![]() ЃЌзМЯпЮЊ
ЃЌзМЯпЮЊ![]() ЃЌШ§ИіЕу
ЃЌШ§ИіЕу![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() жаЧЁгаСНИіЕудк
жаЧЁгаСНИіЕудк![]() ЩЯЃЎ
ЩЯЃЎ
ЃЈ1ЃЉЧѓХзЮяЯп![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉЙ§![]() ЕФжБЯпНЛ
ЕФжБЯпНЛ![]() гк
гк![]() ЃЌ
ЃЌ ![]() СНЕуЃЌЕу
СНЕуЃЌЕу![]() ЮЊ
ЮЊ![]() ЩЯШЮвтвЛЕуЃЌжЄУїЃКжБЯп
ЩЯШЮвтвЛЕуЃЌжЄУїЃКжБЯп![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЕФаБТЪГЩЕШВюЪ§СаЃЎ
ЕФаБТЪГЩЕШВюЪ§СаЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжааФдкдЕуЕФЫЋЧњЯп![]() ЕФгвНЙЕуЮЊ
ЕФгвНЙЕуЮЊ![]() ЃЌгвЖЅЕуЮЊ
ЃЌгвЖЅЕуЮЊ![]() ЃЌЃЈ
ЃЌЃЈ ![]() ЮЊдЕуЃЉ
ЮЊдЕуЃЉ
ЃЈ1ЃЉЧѓЫЋЧњЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯп![]() ЃК
ЃК ![]() гыЫЋЧњЯпКугаСНИіВЛЭЌЕФНЛЕу
гыЫЋЧњЯпКугаСНИіВЛЭЌЕФНЛЕу![]() КЭ
КЭ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com