
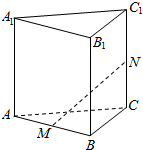
 如图,三棱柱ABC-A1B1C1的棱长都是1,∠BAC=∠BAA1=∠CAA1=60°,点M,N分别是AB,CC1的中点,记$\overrightarrow{AB}$=a,$\overrightarrow{AC}$=b,$\overrightarrow{A{A}_{1}}$=c.
如图,三棱柱ABC-A1B1C1的棱长都是1,∠BAC=∠BAA1=∠CAA1=60°,点M,N分别是AB,CC1的中点,记$\overrightarrow{AB}$=a,$\overrightarrow{AC}$=b,$\overrightarrow{A{A}_{1}}$=c.分析 (1)根据向量加法、减法及数乘的几何意义便可得到$\overrightarrow{MN}=\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AB}+\frac{1}{2}\overrightarrow{A{A}_{1}}$,然后进行向量的数乘运算便可得出$\overrightarrow{MN}=-\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$;
(2)求${\overrightarrow{MN}}^{2}=(-\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}+\frac{1}{2}\overrightarrow{c})^{2}$,然后根据条件进行数量积的运算,便可求出${\overrightarrow{MN}}^{2}$,这样即可得出$|\overrightarrow{MN}|$.
解答 解:(1)$\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}$
=$\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AB}+\frac{1}{2}\overrightarrow{A{A}_{1}}$
=$-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AC}+\frac{1}{2}\overrightarrow{A{A}_{1}}$
=$-\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$;
(2)${\overrightarrow{MN}}^{2}=(-\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}+\frac{1}{2}\overrightarrow{c})^{2}$
=$\frac{1}{4}{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+\frac{1}{4}{\overrightarrow{c}}^{2}-\overrightarrow{a}•\overrightarrow{b}-\frac{1}{2}\overrightarrow{a}•\overrightarrow{c}+\overrightarrow{b}•\overrightarrow{c}$
=$\frac{1}{4}+1+\frac{1}{4}-\frac{1}{2}-\frac{1}{4}+\frac{1}{2}$
=$\frac{5}{4}$;
∴$\overrightarrow{MN}$的模长为$\frac{\sqrt{5}}{2}$.
点评 考查向量加法、减法,及数乘的几何意义,相等向量的概念,以及向量的数乘运算,求向量的平方从而求出向量长度的方法.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | -16 | C. | a2+2a-16 | D. | a2-2a-16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z的虚部为4i | B. | z的共轭复数为1-4i | ||
| C. | |z|=5 | D. | z在复平面内对应的点在第二象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
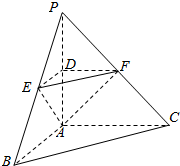 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥BC,AB⊥AC,PA=1,BC=2.D、E、F分别是棱PA、PB、PC的中点,连接DE、DF、EF.
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥BC,AB⊥AC,PA=1,BC=2.D、E、F分别是棱PA、PB、PC的中点,连接DE、DF、EF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com