
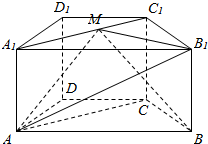
 在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1.
在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1.分析 第 (1)问要证明BC⊥平面A1ACC1,因为考虑到条件里有平面A1ACC1⊥平面ABCD,所以可以考虑面面垂直的性质定理.
第(2)问,几何体B1-AMB为三棱锥,其体积不易直接计算,可以利用等体积法进行转换${V}_{{B}_{1}-AMB}={V}_{M-AB{B}_{1}}$,利用几何体B1-AMB的体积为定值确定M点的位置.
解答  (1)在梯边ABCD中,∵AB∥CD,AD=DC=CB=1,$∠ABC=\frac{π}{3}$,
(1)在梯边ABCD中,∵AB∥CD,AD=DC=CB=1,$∠ABC=\frac{π}{3}$,
所以四边形ABCD为等腰梯形,∴AB=2CD=2,
∴$A{C}^{2}=A{B}^{2}+B{C}^{2}-2AB?BCcos\frac{π}{3}=3$,
∴AB2=AC2+BC2,∴BC⊥AC,
又∵平面A1ACC1⊥平面ABCD,平面A1ACC1∩平面ABCD=AC,
∴BC⊥平面A1ACC1.
(2)因为${A}_{1}{C}_{1}=AC=\sqrt{3}$,所以设${A}_{1}M=λ(0≤λ≤\sqrt{3})$,过M做ME垂直A1B1于E,
∵CC1⊥平面ABCD,∴四棱柱ABCD-A1B1C1D1为直四棱柱,从而平面ABB1A1⊥平面A1B1C1D1,
又平面ABB1A1∩平面A1B1C1D1=A1B1,
所以ME⊥平面A1B1C1D1,
所以ME为M到平面A1B1C1D1的距离.因为△A1ME∽△A1B1C1,
所以$\frac{ME}{{B}_{1}{C}_{1}}=\frac{{A}_{1}M}{{A}_{1}{B}_{1}}∴\frac{ME}{1}=\frac{λ}{2}∴ME=\frac{λ}{2}$,${V}_{{B}_{1}-AMB}={V}_{M-AB{B}_{1}}=\frac{1}{3}×ME×{S}_{{△ABB}_{1}}=\frac{λ}{6}×\frac{1}{2}×1×2=\frac{\sqrt{3}}{12}$.
∴$λ=\frac{\sqrt{3}}{2}$,
从而M点为A1C1的中点.
点评 纵览近几年的高考试题,不难发现立体几何解答题多设置两问,(1)问主要考查空间中的平行、垂直两大位置关系,工具为相关的判定与性质定理,需要注意线线、线面、面面三者之间的相互转化;(2)问多涉及常见几何体的体积、点到面的距离等知识,常以定值或证明的形式出现.预测2015年仍将采用此种模式,需重点关注四棱锥与四棱柱为载体的题型.要注意三个意识,第一为转化与化归的意识,注意线线关系,线面关系,面面关系之间的转化,注意垂直关系,平行关系之间的转化.第二为平面化的思想,即立体几何问题平面化,三是割补意识,将原空间几何体分割或补形,使之成为便于处理的空间几何体.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
 如图,在矩形ABCD中,AB=4,BC=3,沿对角线AC把矩形折成二面角D-AC-B,并且D点在平面ABC内的射影落在AB上.
如图,在矩形ABCD中,AB=4,BC=3,沿对角线AC把矩形折成二面角D-AC-B,并且D点在平面ABC内的射影落在AB上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E,若AB=8,DC=4,则DE=( )
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E,若AB=8,DC=4,则DE=( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (Ⅰ)求过点($\sqrt{3},2\sqrt{2}$)且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程.
(Ⅰ)求过点($\sqrt{3},2\sqrt{2}$)且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 3 | C. | $\sqrt{13}$ | D. | $\sqrt{17}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com