
【题目】在三棱柱ABC﹣A1B1C1中,侧棱BB1⊥底面A1B1C1 , D为AC 的中点,A1B1=BB1=2,A1C1=BC1 , ∠A1C1B=60°. 
(Ⅰ)求证:AB1∥平面BDC1;
(Ⅱ)求多面体A1B1C1DBA的体积.
【答案】(Ⅰ)证明:连B1C交BC1于O,连接OD,在△CAB1中,O,D分别是B1C,AC的中点,∴OD∥AB1 , 而AB1平面BDC1 , OD平面BDC1 , ∴AB1∥平面BDC1;
(Ⅱ)解:连接A1B,作BC的中点E,连接DE,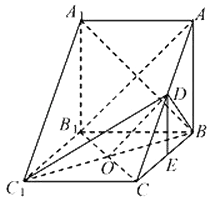
∵A1C1=BC1 , ∠A1C1B=60°,
∴△A1C1B为等边三角形,
∵侧棱BB1⊥底面A1B1C1 ,
∴BB1⊥A1B1 , BB1⊥B1C1 ,
∴A1C1=BC1=A1B=2 ![]() ,
,
∴B1C1=2,
∴A1C12=B1C12+A1B12 ,
∴∠A1B1C1=90°,∴A1B1⊥B1C1 ,
∴A1B1⊥平面B1C1CB,
∵DE∥AB∥A1B1 ,
∴DE⊥平面B1C1CB,
∴DE是三棱锥D﹣BCC1的高,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴多面体A1B1C1DBA的体积V= ![]() ﹣
﹣ ![]() =(
=( ![]() )×2﹣
)×2﹣ ![]() =
= ![]() .
.
【解析】(Ⅰ)证明AB1∥平面BDC1 , 证明OD∥AB1即可;(Ⅱ)利用割补法,即可求多面体A1B1C1DBA的体积.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x+2|﹣|x﹣2|. (Ⅰ)求不等式f(x)>2的解集;
(Ⅱ)若x∈R,f(x)≥t2﹣ ![]() t恒成立,求实数t的取值范围.
t恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的极坐标方程为ρ2cos2θ=18,曲线C2的极坐标方程为θ= ![]() ,曲线C1 , C2相交于A,B两点.
,曲线C1 , C2相交于A,B两点.
(1)求A,B两点的极坐标;
(2)曲线C1与直线  (t为参数)分别相交于M,N两点,求线段MN的长度.
(t为参数)分别相交于M,N两点,求线段MN的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为![]() ,原点到直线
,原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知定点![]() ,是否存在过
,是否存在过![]() 的直线
的直线![]() ,使
,使![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的左顶点?若存在,求出
的左顶点?若存在,求出![]() 的方程:若不存在,请说明理由.
的方程:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的半径为2,圆心在
的半径为2,圆心在![]() 轴的正半轴上,且与直线
轴的正半轴上,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程。
的方程。
(2)在圆![]() 上,是否存在点
上,是否存在点![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,且△
,且△![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标及对应的△
的坐标及对应的△![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,
, ![]() ,函数
,函数 ![]() .
.
(1)求函数f(x)的单调递增区间;
(2)已知a,b,c分别为△ABC内角A,B,C的对边,其中A为锐角, ![]() ,c=1,且f(A)=1,求△ABC的面积S.
,c=1,且f(A)=1,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为 ![]() (∠ACB=
(∠ACB= ![]() ),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ
),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ 
(1)若θ= ![]() ,求△ABC的周长(结果精确到0.01米);
,求△ABC的周长(结果精确到0.01米);
(2)为了使小动物能健康成长,要求所建的三角形露天活动室面积△ABC的面积尽可能大,问当θ为何值时,该活动室面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,则关于函数f(x)有以下四个命题( )
,则关于函数f(x)有以下四个命题( )
①x∈R,f(f(x))=1;
②x0 , y0∈R,f(x0+y0)=f(x0)+f(y0);
③函数f(x)是偶函数;
④函数f(x)是周期函数.
其中真命题的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com