
【题目】在平面直角坐标系中,若![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设(Ⅰ)中曲线![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() (不与
(不与![]() ,
,![]() 重合).若直线
重合).若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,试判断点
,试判断点![]() ,
,![]() ,
,![]() 是否共线,并说明理由.
是否共线,并说明理由.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
第(Ⅰ)问由且![]() 可得点到两定点的距离之和为常数,可得动点轨迹为椭圆;
可得点到两定点的距离之和为常数,可得动点轨迹为椭圆;
第(Ⅱ)问分类讨论直线![]() 的方程,斜率不存在时可直接求出所需点的坐标;斜率存在时则先设出直线方程,联立直线方程与椭圆方程求出交点关系,再求出点
的方程,斜率不存在时可直接求出所需点的坐标;斜率存在时则先设出直线方程,联立直线方程与椭圆方程求出交点关系,再求出点![]() ,利用
,利用![]() 的关系判断即可.
的关系判断即可.
解:(Ⅰ)设![]() ,
,![]() ,则
,则
![]()
![]() .
.
∴动点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点的椭圆,
为焦点的椭圆,
设其方程为![]() ,则
,则![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
∴![]() .∴动点
.∴动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(Ⅱ)①当直线![]() 的斜率不存在时,
的斜率不存在时,![]() :
:![]() ,不妨设
,不妨设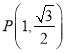 ,
, ,
,
∴直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得![]() .
.
∴![]() .∴点
.∴点![]() ,
,![]() ,
,![]() 共线.
共线.
②当直线![]() 的斜率存在时,设
的斜率存在时,设![]() :
:![]() ,设
,设![]() ,
,![]() .
.
由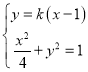 消
消![]() 得
得![]() ,
,
由题意知![]() 恒成立,故
恒成立,故![]() ,
,![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得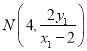 .
.
∴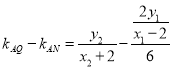
![]() ,
,
上式中的分子![]()
![]()
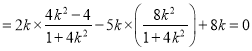 .
.
∴![]() ,∴点
,∴点![]() ,
,![]() ,
,![]() 共线.
共线.
综上可知,点![]() ,
,![]() ,
,![]() 共线.
共线.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年全国掀起了垃圾分类的热潮,垃圾分类已经成为新时尚,同时带动了垃圾桶的销售.某垃圾桶生产和销售公司通过数据分析,得到如下规律:每月生产![]() 只垃圾桶的总成本
只垃圾桶的总成本![]() 由固定成本和生产成本组成,其中固定成本为100万元,生产成本为
由固定成本和生产成本组成,其中固定成本为100万元,生产成本为![]() .
.
(1)写出平均每只垃圾桶所需成本![]() 关于
关于![]() 的函数解析式,并求该公司每月生产多少只垃圾桶时,可使得平均每只所需成本费用最少?
的函数解析式,并求该公司每月生产多少只垃圾桶时,可使得平均每只所需成本费用最少?
(2)假设该类型垃圾桶产销平衡(即生产的垃圾桶都能卖掉),每只垃圾桶的售价为![]() 元,
元,![]() 满足
满足![]() .若当产量为15000只时利润最大,此时每只售价为300元,试求
.若当产量为15000只时利润最大,此时每只售价为300元,试求![]() 的值.(利润
的值.(利润![]() 销售收入
销售收入![]() 成本费用)
成本费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
是否需要志愿 性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人中,需要志愿帮助的老年人的比例?说明理由.
P | 0.0 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为![]() (t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)写出曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C交于A,B两点,且AB的长度为2![]() ,求直线l的普通方程.
,求直线l的普通方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com