
【题目】如图,在正方体![]() 中,点
中,点![]() 为棱
为棱![]() 上一动点(不包括顶点),平面
上一动点(不包括顶点),平面![]() 交
交![]() 于点
于点![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
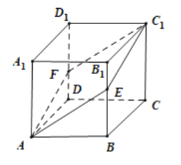
A.存在点![]() ,使得四边形
,使得四边形![]() 为菱形
为菱形
B.存在点![]() ,使得四边形
,使得四边形![]() 的面积最小
的面积最小
C.存在点![]() ,使得
,使得![]() 平面
平面![]()
D.存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() (其中
(其中![]() 为
为![]() 的中点)
的中点)
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,长轴长为
,长轴长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程及离心率;
的标准方程及离心率;
(Ⅱ)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,求证:由点
,求证:由点![]() 构成的曲线
构成的曲线![]() 关于直线
关于直线![]() 对称.
对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线交该椭圆于
轴的直线交该椭圆于![]() ,
,![]() 两点,直线
两点,直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若![]() 的外接圆在
的外接圆在![]() 处的切线与椭圆交另一点于
处的切线与椭圆交另一点于![]() ,且
,且![]() 的面积为
的面积为![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 为
为![]() 的中点,
的中点,![]() .
.
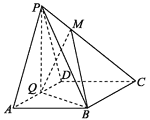
(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,
上,![]() ,试确定
,试确定![]() 的值,使
的值,使![]() 平面
平面![]() ;
;
(3)若![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某盒子中有4个小球,分别写有“中”、“美”、“建”、“交”四个字,从中任取一个小球,有放回抽取,直到“建”、“交”二字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率;利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3,代表“中”、“美”、“建”、“交”着四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了一下18组随机数:
323 213 320 032 132 031 123 330 110
321 120 122 321 221 230 132 322 130
由此可以估计,恰好第三次停止的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象站统计了4月份甲、乙两地的天气温度(单位![]() ),统计数据的茎叶图如图所示,
),统计数据的茎叶图如图所示,
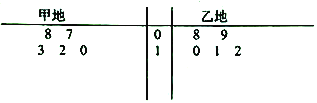
(1)根据所给茎叶图利用平均值和方差的知识分析甲,乙两地气温的稳定性;
(2)气象主管部门要从甲、乙两地各随机抽取一天的天气温度,若甲、乙两地的温度之和大于或等于![]() ,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() =1(a>0,b>0)的一条渐近线方程为2x+y=0,且顶点到渐近线的距离为
=1(a>0,b>0)的一条渐近线方程为2x+y=0,且顶点到渐近线的距离为![]() .
.
(1)求此双曲线的方程;
(2)设P为双曲线上一点,A,B两点在双曲线的渐近线上,且分别位于第一、二象限,若![]() ,求△AOB的面积.
,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018湖南(长郡中学、株洲市第二中学)、江西(九江一中)等十四校高三第一次联考】已知函数![]() (其中
(其中![]() 且
且![]() 为常数,
为常数, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ).
).
(Ⅰ)若函数![]() 的极值点只有一个,求实数
的极值点只有一个,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,若
时,若![]() (其中
(其中![]() )恒成立,求
)恒成立,求![]() 的最小值
的最小值![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为200的调查样本,其中城镇户籍与农村户籍各100人;男性120人,女性80人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图,如图所示,其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
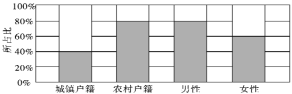
A. 是否倾向选择生育二胎与户籍有关
B. 是否倾向选择生育二胎与性别有关
C. 倾向选择生育二胎的人群中,男性人数与女性人数相同
D. 倾向选择不生育二胎的人群中,农村户籍人数少于城镇户籍人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com