
【题目】已知函数![]() ,
,![]() ,其中e是自然对数的底数.
,其中e是自然对数的底数.
(1)若函数![]() 的极大值为
的极大值为![]() ,求实数a的值;
,求实数a的值;
(2)当a=e时,若曲线![]() 与
与![]() 在
在![]() 处的切线互相垂直,求
处的切线互相垂直,求![]() 的值;
的值;
(3)设函数![]() ,若
,若![]() >0对任意的x
>0对任意的x![]() (0,1)恒成立,求实数a的取值范围.
(0,1)恒成立,求实数a的取值范围.
【答案】(1)a=1;(2)![]() ;(3)[
;(3)[![]() ,
,![]() ).
).
【解析】
(1)利用导数求出![]() 的极大值
的极大值![]() ,即得a的值;
,即得a的值;
(2)由![]() 得到
得到![]() ,设
,设![]() ,根据函数的单调性和
,根据函数的单调性和![]() 得到
得到![]() ;
;
(3)由题得![]() 对任意x
对任意x![]() (0,1)恒成立,设
(0,1)恒成立,设![]() ,得到
,得到![]() 对任意x
对任意x![]() (0,1)恒成立,即
(0,1)恒成立,即![]() ,设
,设![]() ,x
,x![]() (0,1),求出
(0,1),求出![]() 的最大值得解.
的最大值得解.
解:(1)因为![]() ,则
,则![]() ,
,
因为![]() ,所以a>0,
,所以a>0,
则当x![]() (0,e)时,
(0,e)时,![]() ,
,![]() 单调递增,
单调递增,
当x![]() (e,
(e,![]() )时,
)时,![]() ,
,![]() 单调递减,
单调递减,
所以当x=e时,![]() 的极大值
的极大值![]() ,解得a=1;
,解得a=1;
(2)当a=e时,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
由题意知,![]() ,
,
整理得![]() ,
,
设![]() ,则
,则![]() ,所以
,所以![]() 单调递增,
单调递增,
因为![]() ,所以
,所以![]() ;
;
(3)由题意可知,![]() 对任意x
对任意x![]() (0,1)恒成立,
(0,1)恒成立,
整理得![]() 对任意x
对任意x![]() (0,1)恒成立,
(0,1)恒成立,
设![]() ,由(1)可知,
,由(1)可知,![]() 在(0,1)上单调递增,
在(0,1)上单调递增,
且当x![]() (1,
(1,![]() )时,
)时,![]() ,当x
,当x![]() (0,1)时,
(0,1)时,![]() ,
,
若![]() ,则
,则![]() ,
,
若![]() ,因为
,因为![]() ,且
,且![]() 在(0,1)上单调递增,所以
在(0,1)上单调递增,所以![]() ,
,
综上可知,![]() 对任意x
对任意x![]() (0,1)恒成立,即
(0,1)恒成立,即![]() ,
,
设![]() ,x
,x![]() (0,1),则
(0,1),则![]() ,所以
,所以![]() 单调递增,
单调递增,
所以![]() ,即a的取值范围为[
,即a的取值范围为[![]() ,
,![]() ).
).


科目:高中数学 来源: 题型:
【题目】在统计学中,同比增长率一般是指和去年同期相比较的增长率,环比增长率一般是指和前一时期相比较的增长率.2020年2月29日人民网发布了我国2019年国民经济和社会发展统计公报图表,根据2019年居民消费价格月度涨跌幅度统计折线图,下列说法正确的是( )
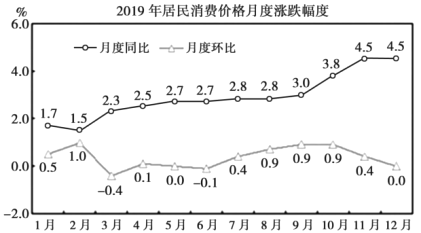
A.2019年我国居民每月消费价格与2018年同期相比有涨有跌
B.2019年我国居民每月消费价格中2月消费价格最高
C.2019年我国居民每月消费价格逐月递增
D.2019年我国居民每月消费价格3月份较2月份有所下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了贯彻落实党中央对新冠肺炎疫情防控工作的部署和要求,坚决防范疫情向校园蔓延,切实保障广大师生身体健康和生命的安全,教育主管部门决定通过电视频道、网络平台等多种方式实施线上教育教学工作.为了了解学生和家长对网课授课方式的满意度,从经济不发达的A城市和经济发达的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如下:
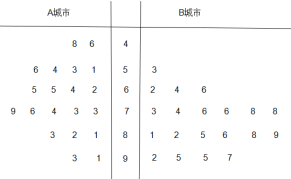
若评分不低于80分,则认为该用户对此授课方式“认可”,否则认为该用户对此授课方式“不认可”.以该样本中A,B城市的用户对此授课方式“认可”的频率分别作为A,B城市用户对此授课方式“认可”的概率.现从A城市和B城市的所有用户中分别随机抽取2个用户,用![]() 表示这4个用户中对此授课方式“认可”的用户个数,则
表示这4个用户中对此授课方式“认可”的用户个数,则![]() __________;用
__________;用![]() 表示从A城市随机抽取2个用户中对此授课方式“认可”的用户个数,则
表示从A城市随机抽取2个用户中对此授课方式“认可”的用户个数,则![]() 的数学期望为_________ .
的数学期望为_________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 中前两项
中前两项![]() 给定,若对于每个正整数
给定,若对于每个正整数![]() ,均存在正整数
,均存在正整数![]() (
(![]() )使得
)使得![]() ,则称数列
,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)若数列![]() 为
为![]() 的等比数列,当
的等比数列,当![]() 时,试问:
时,试问:![]() 与
与![]() 是否相等,并说明数列
是否相等,并说明数列![]() 是否为“
是否为“![]() 数列”;
数列”;
(2)讨论首项为![]() 、公差为
、公差为![]() 的等差数列
的等差数列![]() 是否为“
是否为“![]() 数列”,并说明理由;
数列”,并说明理由;
(3)已知数列![]() 为“
为“![]() 数列”,且
数列”,且![]() ,记
,记![]() ,
,![]() ,其中正整数
,其中正整数![]() , 对于每个正整数
, 对于每个正整数![]() ,当正整数
,当正整数![]() 分别取1、2、
分别取1、2、![]() 、
、![]() 时
时![]() 的最大值记为
的最大值记为![]() 、最小值记为
、最小值记为![]() . 设
. 设![]() ,当正整数
,当正整数![]() 满足
满足![]() 时,比较
时,比较![]() 与
与![]() 的大小,并求出
的大小,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种新的验血技术可以提高血液检测效率.现某专业检测机构提取了![]() 份血液样本,其中只有1份呈阳性,并设计了如下混合检测方案:先随机对其中
份血液样本,其中只有1份呈阳性,并设计了如下混合检测方案:先随机对其中![]() 份血液样本分别取样,然后再混合在一起进行检测,若检测结果为阴性,则对另外3份血液逐一检测,直到确定呈阳性的血液为止;若检测结果呈阳性,测对这
份血液样本分别取样,然后再混合在一起进行检测,若检测结果为阴性,则对另外3份血液逐一检测,直到确定呈阳性的血液为止;若检测结果呈阳性,测对这![]() 份血液再逐一检测,直到确定呈阳性的血液为止.
份血液再逐一检测,直到确定呈阳性的血液为止.
(1)若![]() ,求恰好经过3次检测而确定呈阳性的血液的事件概率;
,求恰好经过3次检测而确定呈阳性的血液的事件概率;
(2)若![]() ,宜采用以上方案检测而确定呈阳性的血液所需次数为
,宜采用以上方案检测而确定呈阳性的血液所需次数为![]() ,
,
①求![]() 的概率分布;
的概率分布;
②求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com