
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 是椭圆
是椭圆![]() 上的一点,从原点
上的一点,从原点![]() 向
向
圆![]() 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点![]() .
.
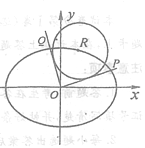
(1)若![]() 点在第一象限,且直线
点在第一象限,且直线![]() 互相垂直,求圆
互相垂直,求圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率存在,并记为
的斜率存在,并记为![]() ,求
,求![]() 的值;
的值;
(3)试问![]() 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)由圆![]() 的方程可知,圆
的方程可知,圆![]() 的半径
的半径![]() ,
,![]() ,由此可求出圆的方程;(2)由已知得直线
,由此可求出圆的方程;(2)由已知得直线![]() 和
和![]() 都与圆
都与圆![]() 相切,化简可得
相切,化简可得![]() ,再利用点在椭圆上,即可求解
,再利用点在椭圆上,即可求解![]() 的值;(3)当直线
的值;(3)当直线![]() 不落在坐标轴上时,设
不落在坐标轴上时,设![]() ,利用直线方程与椭圆的方程联立方程组,得出
,利用直线方程与椭圆的方程联立方程组,得出![]() ,同理
,同理![]() ,由此可求解
,由此可求解![]() 为定值.
为定值.
试题解析:(1)由圆![]() 的方程知圆
的方程知圆![]() 的半径
的半径![]() ,因为直线
,因为直线![]() ,
,![]() 互相垂直,且和圆
互相垂直,且和圆![]() 相切,所以
相切,所以![]() ,即
,即![]() ①
①
又点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ②
②
联立①②,解得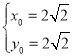 ,所以,所求圆
,所以,所求圆![]() 的方程为
的方程为![]() .
.
(2)因为直线![]()
![]() 和
和![]()
![]() 都与圆
都与圆![]() 相切,所以
相切,所以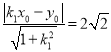 ,
, ,化简得
,化简得![]() ,因为点
,因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,即
,即![]() ,所以
,所以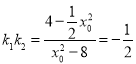 .
.
(3)方法一(1)当直线![]() ,
,![]() 不落在坐标轴上时,设
不落在坐标轴上时,设![]() ,
,![]() ,
,
由(2)知![]() ,所以
,所以![]() ,故
,故![]() .因为
.因为![]() ,
,![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,
,![]() ,
,
即![]() ,
,![]() ,所以
,所以![]() ,
,
整理得![]() ,所以
,所以![]()
所以![]() .
.
方法(二)(1)当直线![]() ,
,![]() 不落在坐标轴上时,设
不落在坐标轴上时,设![]() ,
,![]() ,
,
联立 ,解得
,解得![]() ,
,![]() ,所以
,所以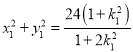 ,
,
同理,得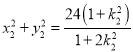 .由(2)
.由(2)![]() ,得
,得![]() ,
,
所以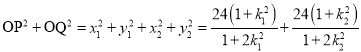
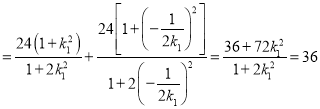 .
.
(2)当直线![]() ,
,![]() 落在坐标轴上时,显然有
落在坐标轴上时,显然有![]() .
.
综上:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆的左焦点为
,椭圆的左焦点为![]() ,椭圆上任意点到
,椭圆上任意点到![]() 的最远距离是
的最远距离是![]() ,过直线
,过直线![]() 与
与![]() 轴的交点
轴的交点![]() 任作一条斜率不为零的直线
任作一条斜率不为零的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(1)求椭圆的方程;
(2)求证:![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(3)求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
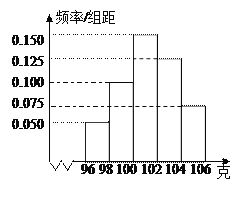
A. 90B. 75C. 60D. 45
查看答案和解析>>
科目:高中数学 来源: 题型:
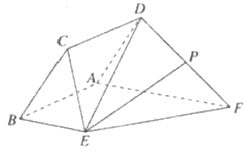
【题目】如图,已知菱形![]() 与直角梯形
与直角梯形![]() 所在的平面互相垂直,其中
所在的平面互相垂直,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点
的中点
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)设![]() 为线段
为线段![]() 上一点,
上一点,![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .已知
.已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程及离心率![]() 的值;
的值;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.

(1)求![]() 的值;
的值;
(2)分别求出甲、乙两组数据的方差![]() 和
和![]() ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的左、右焦点为
)的左、右焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .已知
.已知![]() .
.
(1)求椭圆的离心率;
(2)设![]() 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,经过原点
,经过原点![]() 的直线
的直线![]() 与该圆相切,求直线
与该圆相切,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的 500 名志愿者中随机抽取 100 名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是[20,25),[25,30),[30,35),[35,40),[40,45].
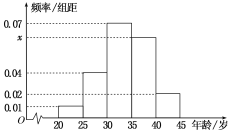
(1)求图中x的值并根据频率分布直方图估计这 500 名志愿者中年龄在[35,40)岁的人数;
(2)在抽出的 100 名志愿者中按年龄采用分层抽样的方法抽取 20 名参加中心广场的宣传活动,再从这 20 名中采用简单随机抽样方法选取 3 名志愿者担任主要负责人.记这 3 名志愿者中“年龄低于 35 岁”的人数为 X,求 X 的分布列及均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com