
分析 (1)由题意可得:点P的轨迹C为椭圆,设标准方程为:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),则c=$\sqrt{3}$,a=2,b2=a2-c2=1,解出可得椭圆的标准方程.
(2)设A(x1,y1),B(x2,y2),直线方程与椭圆联立,化为:(k2+4)x2+2kx-3=0,△>0恒成立,由∠AOB=90°,可得$\overrightarrow{OA}•\overrightarrow{OB}$=x1•x2+y1y2=(1+k2)x1•x2+k(x1+x2)+1=0,把根与系数的关系代入解得k.
(3)在(2)的条件下,x1+x2=$\frac{-2k}{{k}^{2}+4}$=$±\frac{4}{17}$,x1•x2=-$\frac{12}{17}$,利用|AB|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$即可得出.
解答 解:(1)由题意可得:点P的轨迹C为椭圆,设标准方程为:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),
则c=$\sqrt{3}$,a=2,b2=a2-c2=1,可得椭圆的标准方程为:$\frac{{y}^{2}}{4}+{x}^{2}$=1.
(2)设A(x1,y1),B(x2,y2),联立$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{y}^{2}}{4}+{x}^{2}=1}\end{array}\right.$,化为:(k2+4)x2+2kx-3=0,
△=4k2+12(k2+4)>0恒成立,
x1+x2=$\frac{-2k}{{k}^{2}+4}$,x1•x2=$\frac{-3}{{k}^{2}+4}$,
∵∠AOB=90°,∴$\overrightarrow{OA}•\overrightarrow{OB}$=x1•x2+y1y2=x1•x2+(kx1+1)(kx2+1)=(1+k2)x1•x2+k(x1+x2)+1=0,
∴(1+k2)•$\frac{-3}{{k}^{2}+4}$+$\frac{-2{k}^{2}}{{k}^{2}+4}$+1=0,
解得k=$±\frac{1}{2}$.满足△>0.
∴当k=$±\frac{1}{2}$时,能使∠AOB=90°.
(3)在(2)的条件下,x1+x2=$\frac{-2k}{{k}^{2}+4}$=$±\frac{4}{17}$,x1•x2=$\frac{-3}{{k}^{2}+4}$=-$\frac{12}{17}$,
|AB|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{(1+\frac{1}{4})[\frac{16}{1{7}^{2}}-4×(-\frac{12}{17})]}$=$\frac{4\sqrt{65}}{17}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、数量积运算性质、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
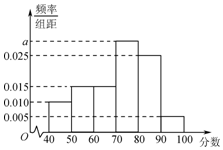 某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),
某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-e•x+1 | B. | y=-x+1 | C. | y=-x | D. | y=-e•x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | $\frac{{\sqrt{10}}}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com