Question

2．已知命题p：?x∈[1，2]，$\sqrt{3}$x²-a≥0，命题q：?x∈[1，3]，使x²-2ax+2=0，若命题p∧q是真命题，求实数a的取值范围．

Answer 1

分析 根据二次函数的最值，一元二次方程解的情况即可求出命题p，q下a的取值范围，再根据p∧q为真命题得到p，q都为真命题，所以对前面所求a的取值范围求交集即可．

解答 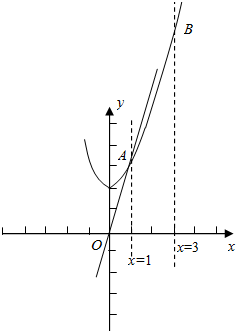解：命题p：若?x∈[1，2]，$\sqrt{3}$x²-a≥0，
只需a≤$\sqrt{3}$x²，x∈[1，2]
y=x²在[1，2]上的最小值为1，∴a≤$\sqrt{3}$；
命题q：?x∈[1，3]，使x²-2ax+2=0，
即方程x²-2ax+2=0在[1，3]上有解，
即2ax=x²+2在[1，3]有解，
即y=2ax和y=x²+2在[1，3]有交点，
画出函数y=2ax和y=x²+2的图象，如图示：
，
显然A（1，3），B（3，11），
当a＜0时：两个函数图象无交点，
a＞0时：当y=2ax过A（1，3）时：a=$\frac{3}{2}$，
当y=2ax过B（3，11）时：a=$\frac{11}{6}$，
∴$\frac{3}{2}$≤a≤$\frac{11}{6}$时函数图象有交点，
即：?x∈[1，3]，使x²-2ax+2=0成立，
若命题p∧q是真命题，则p，q都是真命题；
∴$\frac{3}{2}$≤a≤$\sqrt{3}$．

点评 本题考查了充分必要条件，考查二次函数的性质以及p∧q的真假和p，q真假的关系．