
【题目】已知函数![]() (
(![]() ).
).
(1)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(2)当![]() 时,若在
时,若在![]() (
(![]() )上存在一点
)上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2) 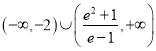 .
.
【解析】试题分析: ![]() 令
令![]() ,
, ![]() ,得
,得![]() ,
,
记![]() ,
, ![]() ,求得导数,利用函数单调性可以求得函数极值点以此判断函数
,求得导数,利用函数单调性可以求得函数极值点以此判断函数![]() 在
在![]() 上的零点个数;
上的零点个数;
![]() 本题不宜分离,因此作差构造函数
本题不宜分离,因此作差构造函数![]() ,利用分类讨论法求函数最小值,由于
,利用分类讨论法求函数最小值,由于![]() ,所以讨论
,所以讨论![]() 与
与![]() 的大小,分三种情况,当
的大小,分三种情况,当![]() ,
, ![]() 的最小值为
的最小值为![]() ,
, ![]() ,
, ![]() 的最小值为
的最小值为![]() ,当
,当![]() ,
, ![]() 的最小值为
的最小值为![]() ,解对应不等式即可。
,解对应不等式即可。
解析:(1)令![]() ,
, ![]() ,得
,得![]() .
.
记![]() ,
, ![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
由此可知![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
且![]() ,
, ![]() .
.
又![]() ,
,
故当![]() 时,
时, ![]() 在区间
在区间![]() 上无零点.
上无零点.
当![]() 或
或![]() 时,
时, ![]() 在区间
在区间![]() 上恰有一个零点.
上恰有一个零点.
当![]() 时,
时, ![]() 在区间
在区间![]() 上有两个零点.
上有两个零点.
(2)在区间![]() (
(![]() )上存在一点
)上存在一点![]() ,使得
,使得![]() 成立等价于函数
成立等价于函数![]() 在区间
在区间![]() 上的最小值小于零.
上的最小值小于零.
![]() .
.
①当![]() ,即
,即![]() 时,
时, ![]() 在区间
在区间![]() 上单调递减,所以
上单调递减,所以![]() 的最小值为
的最小值为![]() ,
,
由![]() ,可得
,可得![]() ,
,
∵![]() ,∴
,∴![]() .
.
②当![]() ,即
,即![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() 的最小值为
的最小值为![]() ,
,
由![]() ,可得
,可得![]() .
.
③当![]() ,即
,即![]() 时,可得
时,可得![]() 的最小值为
的最小值为![]() ,
,
∵![]() ,∴
,∴![]() ,
, ![]() ,
,
此时![]() 不成立.
不成立.
综上所述,实数![]() 的取值范围是
的取值范围是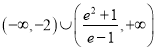 .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1,设p:函数y=loga(x+1)在(0,+∞)上单调递减;q:曲线y=x2+(2a﹣3)x+1与x轴交于不同的两点.如果p且q为假命题,p或q为真命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等差数列{an},满足|a10a11|>a10a11 , 且a102<a112 , Sn为其前n项和,则( )
A.a8+a12>0
B.S1 , S2 , …S19都小于零,S10为Sn的最小值
C.a8+a13<0
D.S1 , S2 , …S20都小于零,S10为Sn的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
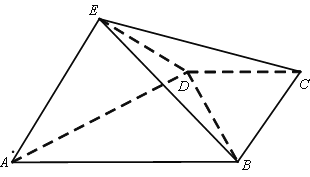
【题目】如图,四棱锥![]() 中,平面
中,平面![]()
![]() 平面
平面![]() ,
,![]() //
// ![]() ,
,![]() ,
,
![]() ,且
,且![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() 使得平面
使得平面![]()
![]() 平面
平面![]() ,请说明理由.
,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx+c在点x=2处取得极值c﹣16.
(1)求a,b的值;
(2)若f(x)有极大值28,求f(x)在[﹣3,3]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马, 田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com