
【题目】设双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:解:设该双曲线方程为 ![]() (a>0,b>0),
(a>0,b>0),
可得它的渐近线方程为y=± ![]() x,焦点为F(c,0),
x,焦点为F(c,0),
点B(0,b)是虚轴的一个端点
∴直线FB的斜率为kFB= ![]() =﹣
=﹣ ![]() ,
,
∵直线FB与直线y= ![]() x互相垂直,
x互相垂直,
∴﹣ ![]() ×
× ![]() =﹣1,得b2=ac
=﹣1,得b2=ac
∵b2=c2﹣a2 ,
∴c2﹣a2=ac,两边都除以a2 , 整理得e2﹣e﹣1=0
解此方程,得e= ![]() ,
,
∵双曲线的离心率e>1,
∴e= ![]() (舍负)
(舍负)
故选:B.
设该双曲线方程为 ![]() (a>0,b>0),得点B(0,b),焦点为F(c,0),直线FB的斜率为﹣
(a>0,b>0),得点B(0,b),焦点为F(c,0),直线FB的斜率为﹣ ![]() .由垂直直线的斜率之积等于﹣1,建立关于a、b、c的等式,变形整理为关于离心率e的方程,解之即可得到该双曲线的离心率.
.由垂直直线的斜率之积等于﹣1,建立关于a、b、c的等式,变形整理为关于离心率e的方程,解之即可得到该双曲线的离心率.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
【题目】命题p:若a、b∈R,则|a|+|b|>1是|a+b|>1的充分而不必要条件;命题q:函数y= ![]() 的定义域是(﹣∞,﹣1]∪[3,+∞),则( )
的定义域是(﹣∞,﹣1]∪[3,+∞),则( )
A.“p或q”为假
B.“p且q”为真
C.p真q假
D.p假q真
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两直线l1:x+8y+7=0和l2:2x+y﹣1=0.
(1)求l1与l2交点坐标;
(2)求过l1与l2交点且与直线x+y+1=0平行的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节电方案,对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:百千瓦![]() 时),将数据按
时),将数据按![]()
![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
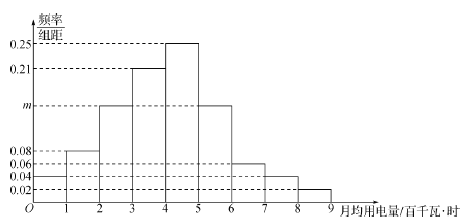
(1)求直方图中![]() 的值;
的值;
(2)设该市有100万户居民,估计全市每户居民中月均用电量不低于6百千瓦![]() 时的人数及每户居民月均用电量的中位数;
时的人数及每户居民月均用电量的中位数;
(3)政府计划对月均用电量在4百千瓦![]() 时以下的用户进行奖励,月均用电量在
时以下的用户进行奖励,月均用电量在![]() 内的用户奖励20元/月,月均用电量在
内的用户奖励20元/月,月均用电量在![]() 内的用户奖励10元/月,月均用电量在
内的用户奖励10元/月,月均用电量在![]() 内的用户奖励2元/月.若该市共有400万户居民,试估计政府执行此计划的年度预算.
内的用户奖励2元/月.若该市共有400万户居民,试估计政府执行此计划的年度预算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com