
分析 (1)设二次函数f(x)的解析式为f(x)=ax2+bx+c,利用待定系数法求解即可.
(2)g(x)=-x2+4x+m,对称轴x=2,g(x)在区间[a,b]上单调,b≤2或a≥2,①1°当b≤2时,2°当a≥2时,列出不等式组,求解m的取值范围为$(-\frac{9}{4},-2]∪$$(-\frac{5}{4},-1]$;
②(法一)设x0为g(x)的零点,则$\left\{\begin{array}{l}g({x_0})=0\\ h({x_0})=0\end{array}\right.$,求出m=0或m=-3,1°当m=0时,求出h(x)所有零点为0,2,4;2°当m=-3时,求出h(x)所有零点为$1,3,2±\sqrt{3}$;
(法二)函数g(x)的零点都是函数h(x)的零点,-(-x2+4x)2+4(-x2+4x)+m=-(-x2+4x+m)(-x2+sx+t),展开对应系数相等求解即可.
解答 解:(1)设二次函数f(x)的解析式为f(x)=ax2+bx+c,
则f(x+2)-f(x)=a(x+2)2+b(x+2)+c-(ax2+bx+c)=4ax+4a+2b…(2分)
由f(x+2)-f(x)=-4x+4得(4a+4)x+4a+2b-4=0恒成立,又f(0)=0
所以$\left\{\begin{array}{l}4a=-4\\ 4a+2b=4\\ c=0\end{array}\right.$,所以$\left\{\begin{array}{l}a=-1\\ b=4\\ c=0\end{array}\right.$,所以f(x)=-x2+4x…(4分)
(2)g(x)=-x2+4x+m,对称轴x=2,g(x)在区间[a,b]上单调,所以b≤2或a≥2
①1°当b≤2时,g(x)在区间[a,b]上单调增,所以$\left\{\begin{array}{l}g(a)=a\\ g(b)=b\end{array}\right.$,即a,b为g(x)=x的两个根,
所以只要g(x)=x有小于等于2两个不相等的实根即可,
所以x2-3x-m=0要满足$\left\{\begin{array}{l}9-4(-m)>0\\{2^2}-6-m≥0\end{array}\right.$,得$-\frac{9}{4}<m≤-2$…(6分)
2°当a≥2时,g(x)在区间[a,b]上单调减,所以$\left\{\begin{array}{l}g(a)=b\\ g(b)=a\end{array}\right.$,即$\left\{\begin{array}{l}-{a^2}+4a+m=b\\-{b^2}+4b+m=a\end{array}\right.$
两式相减得(b-a)(a+b-5)=0,因为b>a,所以a+b-5=0,
所以m=a2-5a+5,$2≤a<\frac{5}{2}$,得$-\frac{5}{4}<m≤-1$…(9分)
综上,m的取值范围为$(-\frac{9}{4},-2]∪$$(-\frac{5}{4},-1]$…(10分)
②(法一)设x0为g(x)的零点,则$\left\{\begin{array}{l}g({x_0})=0\\ h({x_0})=0\end{array}\right.$,即$\left\{\begin{array}{l}-{x_0}^2+4{x_0}+m=0\\-{(-{x_0}^2+4{x_0})^2}+4(-{x_0}^2+4{x_0})+m=0\end{array}\right.$,
即-m2-4m+m=0,得m=0或m=-3…(12分)
1°当m=0时,h(x)=-(-x2+4x)2+4(-x2+4x)=-x(x-4)(x2-4x+4)
所以h(x)所有零点为0,2,4…(14分)
2°当m=-3时,h(x)=-(-x2+4x)2+4(-x2+4x)-3=-(-x2+4x-3)(-x2+4x-1)
(因为必有因式-x2+4x-3,所以容易分解因式)
由-x2+4x-3=0和-x2+4x-1=0得$x=1,3,2±\sqrt{3}$,
所以h(x)所有零点为$1,3,2±\sqrt{3}$…(16分)
(法二)函数g(x)的零点都是函数h(x)的零点,
所以-(-x2+4x)2+4(-x2+4x)+m中必有因式-x2+4x+m,
所以可设:-(-x2+4x)2+4(-x2+4x)+m=-(-x2+4x+m)(-x2+sx+t)
展开对应系数相等得$\left\{\begin{array}{l}m=0\\ s=4\\ t=-4\end{array}\right.$或$\left\{\begin{array}{l}m=-3\\ s=4\\ t=-1\end{array}\right.$(下同法一).
点评 本题考查函数的零点的求法,二次函数的性质,待定系数法以及转化思想的应用,考查计算能力.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
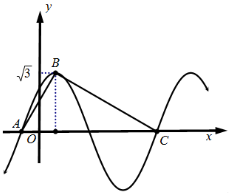 已知函数y=$\sqrt{3}$sin(ωx+$\frac{π}{4}$)(ω>0).
已知函数y=$\sqrt{3}$sin(ωx+$\frac{π}{4}$)(ω>0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{7}{4}$ | C. | $\frac{11}{4}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | $-\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com