解:(I)依题意,求导函数,可得f′(x)=3x
2-2ax-3,
∵
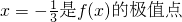
∴f′(-

)=0,∴

+

a-3=0,∴a=4,
∴f(x)=x
3-4x
2-3x,f′(x)=3x
2-8x-3,
令f′(x)=3x
2-8x-3=0,解得x
1=-

,x
2=3,
∴函数在(1,3)上单调减,(3,4)上单调增
而f(1)=-6,f(3)=-18,f(4)=-12,∴f(x)在区间[1,4]上的最大值是f(1)=-6.
(Ⅱ)函数g(x)=bx的图象与函数f(x)的图象恰有3个不同的交点,等价于方程x
3-4x
2-3x=bx恰有3个不等的实数根,
而x=0是方程x
3-4x
2-3x=bx的一个实数根,则方程x
2-4x-3-b=0有两个非零实数根,
则
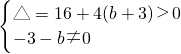
,即b>-7且b≠-3,
故满足条件的b存在,其取值范围是(-7,-3)∪(-3,+∞).
分析:(I)首利用函数的导数与极值的关系求出a的值,确定函数在区间[1,4]上的单调性,求出函数极值的大小并与端点函数值进行比较,即可求出函数的最大值;
(Ⅱ)可以先假设存在,将函数g(x)=bx的图象与函数f(x)的图象恰有3个不同的交点,等价于方程x
3-4x
2-3x=bx恰有3个不等的实数根,进一步转化为方程x
2-4x-3-b=0有两个非零实数根,即可求得结论.
点评:本题考查导数知识的运用,考查函数的单调性、极值与最值,考查图象的交点,熟练运用导数与函数单调性的关系,将图象的交点问题转化为方程根的研究是解题的关键.

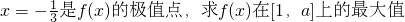 ;
;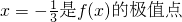
 )=0,∴
)=0,∴ +
+ a-3=0,∴a=4,
a-3=0,∴a=4, ,x2=3,
,x2=3,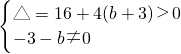 ,即b>-7且b≠-3,
,即b>-7且b≠-3,

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<