设
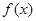
是定义在(0,+∞)上的单调增函数,满足:
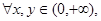
恒有
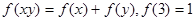
,求:
(Ⅰ)
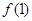
;
(Ⅱ)若
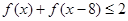
,求
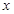
的取值范围。
解:(Ⅰ)∵

,∴
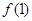
=0。
(Ⅱ)

,从而有
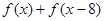
≤f(9),
即
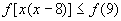
,∵
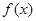
是(0,+∞)上的增函数,故
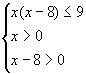
,解之得:8<x≤9。
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
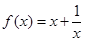
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明
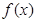
在
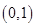
上是减函数;
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设函数

.
(1)当
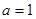
,
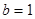
时,求所有使
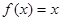
成立的
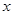
的值。
(2)若
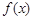
为奇函数,求证:
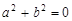
;
(3)设常数

<
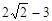
,且对任意
x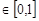
,
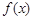
<0恒成立,求实数

的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
f(
x)=
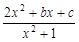
(
b<0)的值域是[1,3],
(1)求
b、
c的值;
(2)判断函数
F(
x)=lg
f(
x),当
x∈[-1,1]时的单调性,并证明你的结论;
(3)若
t∈R,求证:lg
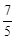
≤
F(|
t-
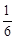
|-|
t+
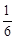
|)≤lg
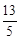
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)
已知函数
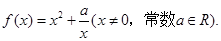
(Ⅰ)当
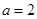
时,解不等式
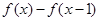
>
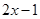
;
(Ⅱ)讨论函数
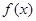
的奇偶性,并说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
由函数
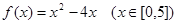
的最大值与最小值可以得其值域为 ( )
查看答案和解析>>

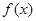 是定义在(0,+∞)上的单调增函数,满足:
是定义在(0,+∞)上的单调增函数,满足: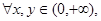 恒有
恒有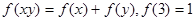 ,求:
,求: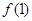 ;
;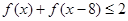 ,求
,求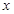 的取值范围。
的取值范围。 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案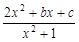 (b<0)的值域是[1,3],
(b<0)的值域是[1,3],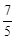 ≤F(|t-
≤F(|t-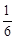 |-|t+
|-|t+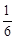 |)≤lg
|)≤lg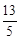 .
.