
【题目】学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球.乙箱子里装有1个白球、2个黑球.每次游戏从这两个箱子里随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏结束后,①摸出3个白球的概率?②获奖的概率?
(2)求在2次游戏中获奖次数X的分布列及数学期望E(X).
【答案】
(1)解:设“摸出3个白球”为事件A,则必须从甲箱子里摸出2个白球,从乙箱子里摸出1个白球与1个黑球.
∴P(A)= ![]() =
= ![]() .
.
②设“获奖”为事件B,B包括两种情况:一种是从甲箱子里摸出1个白球与一个黑球,从乙箱子里摸出1个白球与1个黑球;另一种是从甲箱子里摸出2个白球,从乙箱子里3个球中摸出2个球.
则P(B)= ![]() =
= ![]()
(2)解:由(1)②可知:在1次游戏中,“获奖”的概率P= ![]() ,因此X~B
,因此X~B ![]() .P(X=k)=
.P(X=k)= ![]() ,(k=0,1,2).
,(k=0,1,2).
X | 0 | 1 | 2 |
P |
|
|
|
∴E(X)= ![]() =75
=75
【解析】(1)设“摸出3个白球”为事件A,则必须从甲箱子里摸出2个白球,从乙箱子里摸出1个白球与1个黑球.可得P(A)= ![]() .②设“获奖”为事件B,B包括两种情况:一种是从甲箱子里摸出1个白球与一个黑球,从乙箱子里摸出1个白球与1个黑球;另一种是从甲箱子里摸出2个白球,从乙箱子里3个球中摸出2个球.可得P(B).(2)由(1)②可知:在1次游戏中,“获奖”的概率P=
.②设“获奖”为事件B,B包括两种情况:一种是从甲箱子里摸出1个白球与一个黑球,从乙箱子里摸出1个白球与1个黑球;另一种是从甲箱子里摸出2个白球,从乙箱子里3个球中摸出2个球.可得P(B).(2)由(1)②可知:在1次游戏中,“获奖”的概率P= ![]() ,因此X~B
,因此X~B ![]() .利用P(X=k)=
.利用P(X=k)= ![]() ,(k=0,1,2),即可得出分布列与数学期望.
,(k=0,1,2),即可得出分布列与数学期望.
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,当∠xOy=α,且α∈(0, ![]() )∪(
)∪( ![]() ,π)时,定义平面坐标系xOy为α﹣仿射坐标系.在α﹣仿射坐标系中,任意一点P的斜坐标这样定义:
,π)时,定义平面坐标系xOy为α﹣仿射坐标系.在α﹣仿射坐标系中,任意一点P的斜坐标这样定义: ![]() 、
、 ![]() 分别为与x轴、y轴正向相同的单位向量,若
分别为与x轴、y轴正向相同的单位向量,若 ![]() =x
=x ![]() +y
+y ![]() ,则记为
,则记为 ![]() =(x,y).现给出以下说法:
=(x,y).现给出以下说法:
①在α﹣仿射坐标系中,已知 ![]() =(1,2),
=(1,2), ![]() =(3,t),若
=(3,t),若 ![]() ∥
∥ ![]() ,则t=6;
,则t=6;
②在α﹣仿射坐标系中,若 ![]() =(
=( ![]() ,
, ![]() ),若
),若 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),则
),则 ![]()
![]() =0;
=0;
③在60°﹣仿射坐标系中,若P(2,﹣1),则| ![]() |=
|= ![]() ;
;
其中说法正确的有 . (填出所有说法正确的序号)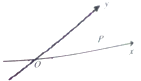
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明12+22+…+(n﹣1)2+n2+(n﹣1)2+…+22+12═ ![]() 时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
A.(k+1)2+2k2
B.(k+1)2+k2
C.(k+1)2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA垂直于矩形ABCD所在的平面,M,N分别是AB,PC的中点,若∠PDA=45°, 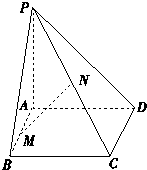
(1)求证:MN∥平面PAD且MN⊥平面PCD.
(2)探究矩形ABCD满足什么条件时,有PC⊥BD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司研究开发了一种新产品,生产这种新产品的年固定成本为150万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() (万元),
(万元),  .每件产品售价为500元.该新产品在市场上供不应求可全部卖完.
.每件产品售价为500元.该新产品在市场上供不应求可全部卖完.
(Ⅰ)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)当年产量为多少千件时,该公司在这一新产品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】探究函数![]() 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成以下的问题.
函数![]() 在区间(0,2)上递减;
在区间(0,2)上递减;
函数![]() 在区间 上递增.
在区间 上递增.
当![]() 时,
时, ![]() .
.
证明:函数![]() 在区间(0,2)递减.
在区间(0,2)递减.
思考:函数![]() 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2009年至2015年农村居民家庭人均纯收入y(单位:千元)的数据如表:
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2009年至2015年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2017年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: 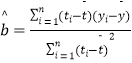 .
. ![]() .
.
参考数据:(﹣3)×(﹣1.4)+(﹣2)×(﹣1)+(﹣1)×(﹣0.7)+1×0.5+2×0.9+3×1.6=14.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,设函数
,设函数![]() ,且
,且![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将![]() 的图象向左平移
的图象向左平移![]() (
(![]() )个单位后得到函数
)个单位后得到函数![]() 的图象.若
的图象.若![]() 的图象上各最高点到点
的图象上各最高点到点![]() 的距离的最小值为1,求
的距离的最小值为1,求![]() 的单调增区间.
的单调增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com