
 与不等式(x-a)(x-b)≤0的解集相同;
与不等式(x-a)(x-b)≤0的解集相同; 与x2-2x<3(x-1)的解集相同.
与x2-2x<3(x-1)的解集相同. 的解集中,故③不正确.
的解集中,故③不正确. 即 x2-2x>3(x-1),故④不正确.
即 x2-2x>3(x-1),故④不正确.

 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
 |
| y |
. |
| x |
. |
| y |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-a |
| x-b |
| x2-2x |
| x-1 |
查看答案和解析>>
科目:高中数学 来源:2010-2011年黑龙江省高一下学期期中考试数学 题型:选择题
有如下几个命题:
①如果 是方程
是方程 的两个实根且
的两个实根且 ,那么不等式
,那么不等式 的解集为
的解集为 ;
;
②当 时,二次不等式
时,二次不等式 的解集为
的解集为 ;
;
③ 与不等式
与不等式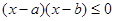 的解集相同;
的解集相同;
④ 与
与 的解集相同.
的解集相同.
其中正确命题的个数是( )
A.3 B.2 C.1 D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
有如下几个命题:
①如果![]() 是方程
是方程![]() 的两个实根且
的两个实根且![]() ,那么不等式
,那么不等式![]() 的解集为
的解集为![]() ;
;
②当![]() 时,二次不等式
时,二次不等式![]() 的解集为
的解集为![]() ;
;
③![]() 与不等式
与不等式![]() 的解集相同;
的解集相同;
④![]() 与
与![]() 的解集相同.
的解集相同.
其中正确命题的个数是( )
A.3 B.2 C.1 D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com