
【题目】如图所示,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 为椭圆
为椭圆![]() 上位于第一象限上的点,
上位于第一象限上的点,![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .
.
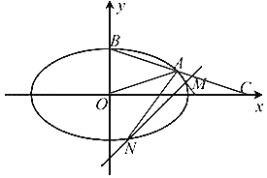
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设直线![]() 过椭圆
过椭圆![]() 的右焦点,且与椭圆
的右焦点,且与椭圆![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 在直线
在直线![]() 的同侧),若
的同侧),若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() 1;(Ⅱ)x﹣y﹣2
1;(Ⅱ)x﹣y﹣2![]() 0.
0.
【解析】
(Ⅰ)运用椭圆的离心率公式和![]() 、
、![]() 、
、![]() 的关系,结合三角形的面积公式和线段的中点坐标公式,解方程可得
的关系,结合三角形的面积公式和线段的中点坐标公式,解方程可得![]() 、
、![]() ,进而得到所求椭圆方程;
,进而得到所求椭圆方程;
(Ⅱ)求得![]() 的坐标和右焦点坐标,运用等腰三角形的性质,可得线
的坐标和右焦点坐标,运用等腰三角形的性质,可得线![]() 、
、![]() 的斜率互为相反数,设直线
的斜率互为相反数,设直线![]() ,联立椭圆方程
,联立椭圆方程![]() ,运用韦达定理,求得
,运用韦达定理,求得![]() ,同理可得
,同理可得![]() ,再由直线的斜率公式,化简整理,即可得到
,再由直线的斜率公式,化简整理,即可得到![]() ,进而得到所求直线方程.
,进而得到所求直线方程.
(Ⅰ)椭圆![]() 的离心率为
的离心率为![]() ,
,
即![]() ,可得
,可得![]() ,
,![]() ,
,
由![]() ,可得
,可得 为
为![]() 的中点,
的中点,
所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() 1;
1;
(Ⅱ)由(Ⅰ)可得![]() ,右焦点为
,右焦点为![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,直线
,直线![]() 、
、![]() 的斜率互为相反数,
的斜率互为相反数,
设直线![]() ,联立椭圆方程
,联立椭圆方程![]() ,
,
消去![]() ,可得
,可得![]() ,
,
设![]() 、
、![]() ,则
,则![]() ,所以
,所以![]() ,
,
将![]() 换为
换为![]() ,同理可得
,同理可得![]() ,
,![]() ,
,![]() ,
,
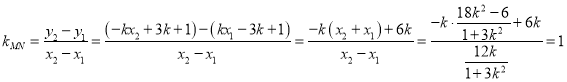 ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】如图,已知函数![]() 的图象与y轴交于点
的图象与y轴交于点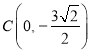 ,与x轴交于A,B两点,其中
,与x轴交于A,B两点,其中![]() ,
,![]() .
.

(1)求函数![]() 的解析式;
的解析式;
(2)将函数![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象,求函数
的图象,求函数![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知等边![]() 的边长为3,点
的边长为3,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() .如图2,将
.如图2,将![]() 沿
沿![]() 折起到
折起到![]() 的位置.
的位置.
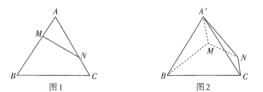
(1)求证:平面![]() 平面
平面![]() ;
;
(2)给出三个条件:①![]() ;②二面角
;②二面角![]() 大小为
大小为![]() ;③
;③![]() .在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段
.在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
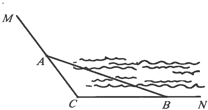
(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
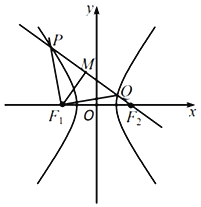
【题目】设双曲线![]() 的左、右焦点分别为F1,F2,过点F2的直线分别交双曲线左、右两支于点P,Q,点M为线段PQ的中点,若P,Q,F1都在以M为圆心的圆上,且
的左、右焦点分别为F1,F2,过点F2的直线分别交双曲线左、右两支于点P,Q,点M为线段PQ的中点,若P,Q,F1都在以M为圆心的圆上,且![]() ,则双曲线C的离心率为( )
,则双曲线C的离心率为( )
A.![]() B.2
B.2![]() C.
C.![]() D.2
D.2![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年上半年,随着新冠肺炎疫情在全球蔓延,全球超过
年上半年,随着新冠肺炎疫情在全球蔓延,全球超过![]() 个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为
个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为![]() 年第一季度企业成立年限与倒闭分布情况统计表:
年第一季度企业成立年限与倒闭分布情况统计表:
企业成立年份 | 2019 | 2018 | 2017 | 2016 | 2015 |
企业成立年限 | 1 | 2 | 3 | 4 | 5 |
倒闭企业数量(万家) | 5.23 | 4.70 | 3.72 | 3.12 | 2.42 |
倒闭企业所占比例 | 21.8% | 19.6% | 15.5% | 13.0% | 10.1% |
根据上表,给出两种回归模型:
模型①:建立曲线型回归模型![]() ,求得回归方程为
,求得回归方程为![]() ;
;
模型②:建立线性回归模型![]() .
.
(1)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)根据下列表格中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测
,并选择拟合精度更高、更可靠的模型,预测![]() 年成立的企业中倒闭企业所占比例(结果保留整数).
年成立的企业中倒闭企业所占比例(结果保留整数).
回归模型 | 模型① | 模型② |
回归方程 |
|
|
|
|
参考公式: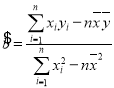 ,
,![]() ;
;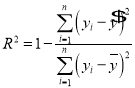 .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
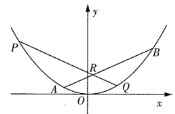
【题目】如图,斜率为![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,已知点
两点,已知点![]() 的横坐标比点
的横坐标比点![]() 的横坐标大4,直线
的横坐标大4,直线![]() 交线段
交线段![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
(1)若点![]() 的横坐标等于0,求
的横坐标等于0,求![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() |2x﹣3|,g(x)
|2x﹣3|,g(x)![]() |2x+a+b|.
|2x+a+b|.
(1)解不等式f(x)![]() x2;
x2;
(2)当a![]() 0,b
0,b![]() 0时,若F(x)
0时,若F(x)![]() f(x)+g(x)的值域为[5,+∞),求证:
f(x)+g(x)的值域为[5,+∞),求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“2019曹娥江国际马拉松”在上虞举行,现要选派5名志愿者服务于![]() 四个不同的运动员救助点,每个救助点至少分配1人,若志愿者甲要求不到A救助点,则不同的分派方案有________种.
四个不同的运动员救助点,每个救助点至少分配1人,若志愿者甲要求不到A救助点,则不同的分派方案有________种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com