
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 依题意建立直角坐标系,加上点C在∠AOB内的限制,可得点C的坐标,在直角三角形中由正切函数的定义可求解
解答 解:因为$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$,且$\overrightarrow{OA}•\overrightarrow{OB}=0$,点C在∠AOB内,$\overrightarrow{OA}$与$\overrightarrow{OC}$夹角为30°,故可建立直角坐标系如图所示.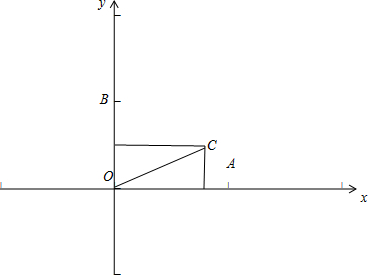
$\overrightarrow{OA}=(1.0).\overrightarrow{OB}=(0,1)$,∵$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$,(m,n∈R),∴$\overrightarrow{OC}=(m,n)$⇒C(m,n),
∵$\overrightarrow{OA}$与$\overrightarrow{OC}$夹角为300,∴tan30°=$\frac{n}{m}=\frac{\sqrt{3}}{3}$
故选:A..
点评 本题为向量的基本运算,建立直角坐标系,利用坐标解决问题是一种常用的处理向量运算的方法,属基础题.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:填空题
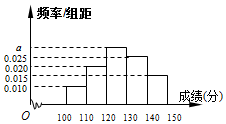 某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在[100,150]的1000名学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩在[120,130)内的学生共有300人.
某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在[100,150]的1000名学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩在[120,130)内的学生共有300人.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com