
【题目】设函数f(x)=lnx﹣ ![]() ax2﹣bx
ax2﹣bx
(1)当a=b= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)当a=0,b=﹣1时,方程f(x)=mx在区间[1,e2]内有唯一实数解,求实数m的取值范围.
【答案】
(1)解:依题意,知f(x)的定义域为(0,+∞),
当a=b= ![]() 时,f(x)=lnx﹣
时,f(x)=lnx﹣ ![]() x2﹣
x2﹣ ![]() x,
x,
∴f′(x)= ![]() ,
,
令f′(x)=0,解得:x=1或x=﹣2(舍去),经检验,x=1是方程的根.
当0<x<1时,f′(x)>0,当x>1时,f′(x)<0,
所以f(x)的单调递增区间是(0,1),单调递减区间是(1,+∞)
(2)解:当a=0,b=﹣1时,f(x)=lnx+x,
由f(x)=mx得mx=lnx+x,
又因为x>0,所以m=1+ ![]() ,
,
要使方程f(x)=mx在区间[1,e2]内有唯一实数解,
只需m=1+ ![]() 有唯一实数解,
有唯一实数解,
令g(x)=1+ ![]() (x>0),∴g′(x)=
(x>0),∴g′(x)= ![]() (x>0),
(x>0),
由g′(x)>0,得:0<x<e,由g′(x)<0,得x>e,
所以g(x)在区间[1,e]上是增函数,在区间[e,e2]上是减函数,
g(1)=1+ ![]() =1,g(e2)=1+
=1,g(e2)=1+ ![]() =1+
=1+ ![]() ,
,
g(e)=1+ ![]() =1+
=1+ ![]() ,
,
所以m=1+ ![]() 或1≤m<1+
或1≤m<1+ ![]()
【解析】(1)将a,b的值代入,求出函数f(x)的表达式,导数,从而求出函数的单调区间;(2)将a,b的值代入函数的表达式,问题转化为只需m=1+ ![]() 有唯一实数解,求出函数y=g(x)=1+
有唯一实数解,求出函数y=g(x)=1+ ![]() 的单调性,从而求出m的范围.
的单调性,从而求出m的范围.
【考点精析】关于本题考查的利用导数研究函数的单调性,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能得出正确答案.
在这个区间单调递减才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子![]() 米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子
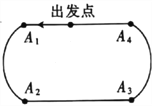
米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子![]() 米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过
米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过![]() 个直道与弯道的交接口
个直道与弯道的交接口![]() .已知某男子速滑运动员顺利通过每个交接口的概率均为
.已知某男子速滑运动员顺利通过每个交接口的概率均为![]() ,摔倒的概率均为
,摔倒的概率均为![]() .假定运动员只有在摔倒或到达终点时才停止滑行,现在用
.假定运动员只有在摔倒或到达终点时才停止滑行,现在用![]() 表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
(1)求该运动员停止滑行时恰好已顺利通过![]() 个交接口的概率;
个交接口的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=4,点F( ![]() ,0),以线段MF为直径的圆内切于圆O,记点M的轨迹为C
,0),以线段MF为直径的圆内切于圆O,记点M的轨迹为C
(1)求曲线C的方程;
(2)若过F的直线l与曲线C交于A,B两点,问:在x轴上是否存在点N,使得 ![]() 为定值?若存在,求出点N坐标;若不存在,说明理由.
为定值?若存在,求出点N坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面推理过程中使用了类比推理方法,其中推理正确的是( )
A. 平面内的三条直线![]() ,若
,若![]() ,则
,则![]() .类比推出:空间中的三条直线
.类比推出:空间中的三条直线![]() ,若
,若![]() ,则
,则![]()
B. 平面内的三条直线![]() ,若
,若![]() ,则
,则![]() .类比推出:空间中的三条向量
.类比推出:空间中的三条向量![]() ,若
,若![]() ,则
,则![]()
C. 在平面内,若两个正三角形的边长的比为![]() ,则它们的面积比为
,则它们的面积比为![]() .类比推出:在空间中,若两个正四面体的棱长的比为
.类比推出:在空间中,若两个正四面体的棱长的比为![]() ,则它们的体积比为
,则它们的体积比为![]()
D. 若![]() ,则复数
,则复数![]() .类比推理:“若
.类比推理:“若![]() ,则
,则![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项都是正数的数列{an}的前n项和为Sn , Sn=an2+ ![]() an , n∈N*
an , n∈N*
(1)求数列{an}的通项公式;
(2)设数列{bn}满足:b1=1,bn﹣bn﹣1=2an(n≥2),求数列{ ![]() }的前n项和Tn
}的前n项和Tn
(3)若Tn≤λ(n+4)对任意n∈N*恒成立,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种型号汽车四个轮胎半径相同,均为R=40cm,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为l=280cm (假定四个轮胎中心构成一个矩形).当该型号汽车开上一段上坡路ABC(如图(1)所示,其中∠ABC=a( ![]() ),且前轮E已在BC段上时,后轮中心在F位置;若前轮中心到达G处时,后轮中心在H处(假定该汽车能顺利驶上该上坡路).设前轮中心在E和G处时与地面的接触点分别为S和T,且BS=60cm,ST=100cm.(其它因素忽略不计)
),且前轮E已在BC段上时,后轮中心在F位置;若前轮中心到达G处时,后轮中心在H处(假定该汽车能顺利驶上该上坡路).设前轮中心在E和G处时与地面的接触点分别为S和T,且BS=60cm,ST=100cm.(其它因素忽略不计) 
(1)如图(2)所示,FH和GE的延长线交于点O,求证:OE=40cot ![]() (cm);
(cm);
(2)当a= ![]() π时,后轮中心从F处移动到H处实际移动了多少厘米?(精确到1cm)
π时,后轮中心从F处移动到H处实际移动了多少厘米?(精确到1cm)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)排成前后两排,前排3人,后排4人;(2)全体站成一排,甲不站排头也不站排尾;
(3)全体站成一排,女生必须站在一起;(4)全体站成一排,男生互不相邻.(用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com