
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据垂直于同一直线的两平面平行,判断①是否正确;
利用线线平行,线面平行,面面平行的转化关系,判断②是否正确;
借助图象,分别过两平行线中一条的二平面位置关系部确定,判断③的正确性;
根据垂直于同一平面的两平面位置关系部确定来判断④是否正确.
解答 解:当α、β不平行时,不存在直线a与α、β都垂直,∴a⊥α,a⊥β⇒α∥β,故①正确;
对②,∵a∥b,a?α,b?β,a∥β,b∥α时,α、β位置关系不确定②不正确;
对③,异面直线a,b.∴a过上一点作c∥b;过b上一点作d∥a,则 a与c相交;b与d相交,根据线线平行⇒线面平行⇒面面平行,正确
对④,∵γ⊥α,γ⊥β,α、β可以相交也可以平行,∴不正确.
故选B.
点评 本题考查面面平行的判定.通常利用线线、线面、面面平行关系的转化判定.


科目:高中数学 来源: 题型:选择题
| A. | 对任意x∈R,使得x2<0 | B. | 不存在x∈R,使得x2<0 | ||
| C. | 存在x0∈R,都有$x_0^2≥0$ | D. | 存在x0∈R,都有$x_0^2<0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
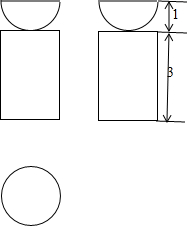 如图是一个组合体的三视图,根据图中数据,可得该几何体的体积是( )
如图是一个组合体的三视图,根据图中数据,可得该几何体的体积是( )| A. | $\frac{38π}{3}$ | B. | $\frac{19π}{3}$ | C. | $\frac{13π}{3}$ | D. | $\frac{11π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
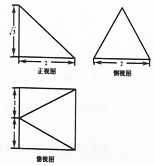 某几何体的三视图如图所示(单位:cm),则该几何体的体积是$\frac{4\sqrt{3}}{3}$(单位:cm3),表面积是8+$\sqrt{3}$+$\sqrt{7}$(单位:cm2)
某几何体的三视图如图所示(单位:cm),则该几何体的体积是$\frac{4\sqrt{3}}{3}$(单位:cm3),表面积是8+$\sqrt{3}$+$\sqrt{7}$(单位:cm2)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com