
【题目】已知函数![]() 的定义域为
的定义域为![]() ,其中
,其中![]() 为常数;
为常数;
(1)若![]() ,且
,且![]() 是奇函数,求
是奇函数,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函数
,函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() ,在
,在![]() 上存在
上存在![]() 个点
个点![]()
![]() ,满足
,满足![]() ,
, ![]() ,
,
![]() ,使得
,使得![]() ,
,
求实数![]() 的取值范围;
的取值范围;
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)因为函数为奇函数,根据奇函数定义可得可得![]() 对任意
对任意![]() 恒成立,变形可得
恒成立,变形可得![]() 对任意
对任意![]() 恒成立,可求
恒成立,可求![]() ;(2)将函数
;(2)将函数![]() 的解析式讨论去掉绝对值号,
的解析式讨论去掉绝对值号,  。两段函数的对称轴都为
。两段函数的对称轴都为![]() ,因为
,因为![]() 。讨论
。讨论 ![]() 与-1的大小,可得两段二次函数在区间
与-1的大小,可得两段二次函数在区间![]() 上的单调性,求得最小值。得最小值
上的单调性,求得最小值。得最小值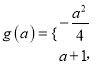 ,求两段的取值范围,取较大的为最大值。(3)由(2)可知
,求两段的取值范围,取较大的为最大值。(3)由(2)可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,所以
上单调递减,所以![]() ,由绝对值不等式可得
,由绝对值不等式可得![]() ,所以
,所以![]() ,整理得
,整理得![]() ,解得
,解得![]() 为所求.
为所求.
试题解析:解:(1)∵![]() 是奇函数,∴
是奇函数,∴![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() ,即
,即![]() 对任意
对任意![]() 恒成立,∴
恒成立,∴![]() ;
;
(2)
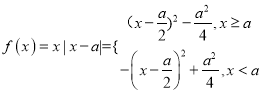 ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
, ![]()
①当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上递减,在
上递减,在![]() 递增,
递增, ![]()
②当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增, ![]()
综上所述, 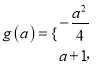 ,
,
若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]()
∴当![]() 时,
时, ![]()
(3)∵![]() ,且
,且![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]()
而![]()
要使满足条件的点存在,必须且只需![]() ,即
,即![]() ,解得
,解得![]() 为所求.
为所求.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知幂函数y=f(x)的图象过点(8,m)和(9,3).
(Ⅰ)求m的值;
(Ⅱ)若函数g(x)=logaf(x)(a>0,a≠1)在区间[16,36]上的最大值比最小值大1,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元.如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8-200=1000(元).设购买某商品得到的实际折扣率![]() .设某商品标价为
.设某商品标价为![]() 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为![]() .
.
(Ⅰ)写出当![]() 时,
时, ![]() 关于
关于![]() 的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
(Ⅱ)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() (万元),若年产量不足
(万元),若年产量不足![]() 千件,
千件, ![]() 的图像是如图的抛物线,此时
的图像是如图的抛物线,此时![]() 的解集为
的解集为![]() ,且
,且![]() 的最小值是
的最小值是![]() ,若年产量不小于
,若年产量不小于![]() 千件,
千件, ![]() ,每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完;
,每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完;
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x2+2(k﹣1)x+k+5.
(1)求函数f(x)在[0,3]上最大值;
(2)若函数f(x)在[0,3]上有零点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,侧面
为矩形,侧面![]() 为正三角形,且平面
为正三角形,且平面![]()
![]() 平面,
平面, ![]() 为
为![]() 中点,
中点, ![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若二面角![]() 的平面角大小
的平面角大小![]() 满足
满足![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A、B、C三种家电,经市场调查决定调整生产方案,计划本季度(按不超过480个工时计算)生产A、B、C三种家电共120台,其中A家电至少生产20台,已知生产A、B、C三种家电每台所需的工时分别为3、4、6个工时,每台的产值分别为20、30、40千元,则按此方案生产,此季度最高产值为( )千元.
A. 3600 B. 350 C. 4800 D. 480
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{![]() }的前n项和为Sn,公差d>0,且
}的前n项和为Sn,公差d>0,且![]() ,
, ![]() ,公比为q(0<q<1)的等比数列{
,公比为q(0<q<1)的等比数列{![]() }中,
}中, ![]()
(1)求数列{![]() },{
},{![]() }的通项公式
}的通项公式![]() ,
, ![]() ;
;
(2)若数列{![]() }满足
}满足![]() ,求数列{
,求数列{![]() }的前n项和Tn。
}的前n项和Tn。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com