
【题目】如图,A,B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上. 
(1)若 ![]() =
= ![]() ,
, ![]() =1,求
=1,求 ![]() 的值;
的值;
(2)若EF2=FAFB,证明:EF∥CD.
【答案】
(1)解:∵A,B,C,D四点共圆,
∴∠ECD=∠EAB,∠EDC=∠B
∴△EDC∽△EBA,可得 ![]() =
= ![]() =
= ![]() ,
,
∴ ![]()
![]() =(
=( ![]() )2,即
)2,即 ![]()
![]() =(
=( ![]() )2
)2
∴ ![]() =
= ![]()
(2)解:证明:∵EF2=FAFB,
∴ ![]() =
= ![]() ,
,
又∵∠EFA=∠BFE,
∴△FAE∽△FEB,可得∠FEA=∠EBF,
又∵A,B,C,D四点共圆,
∴∠EDC=∠EBF,
∴∠FEA=∠EDC,
∴EF∥CD.
【解析】(1)根据圆内接四边形的性质,可得∠ECD=∠EAB,∠EDC=∠B,从而△EDC∽△EBA,所以有 ![]() =
= ![]() =
= ![]() ,利用比例的性质可得
,利用比例的性质可得 ![]()
![]() =(
=( ![]() )2 , 得到
)2 , 得到 ![]() =
= ![]() ;(2)根据题意中的比例中项,可得
;(2)根据题意中的比例中项,可得 ![]() =
= ![]() ,结合公共角可得△FAE∽△FEB,所以∠FEA=∠EBF,再由(I)的结论∠EDC=∠EBF,利用等量代换可得∠FEA=∠EDC,内错角相等,所以EF∥CD.
,结合公共角可得△FAE∽△FEB,所以∠FEA=∠EBF,再由(I)的结论∠EDC=∠EBF,利用等量代换可得∠FEA=∠EDC,内错角相等,所以EF∥CD.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB=2,CD=4,BC= ![]() ,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得
,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得 ![]() =λ成立,那么实数λ的取值范围为 .
=λ成立,那么实数λ的取值范围为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,以原点O为顶点,以y轴为对称轴的抛物线E的焦点为F(0,1),点M是直线l:y=m(m<0)上任意一点,过点M引抛物线E的两条切线分别交x轴于点S,T,切点分别为B,A.
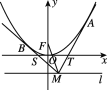
(1)求抛物线E的方程;
(2)求证:点S,T在以FM为直径的圆上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A,B,C的对边分别是a,b,c,3sin2C+8sin2A=11sinAsinC,且c<2a.
(1)求证:△ABC为等腰三角形
(2)若△ABC的面积为8 ![]() .且sinB=
.且sinB= ![]() ,求BC边上的中线长.
,求BC边上的中线长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() =1(a>b>0)的左、右顶点分别为A,B,焦距为2
=1(a>b>0)的左、右顶点分别为A,B,焦距为2 ![]() ,直线x=﹣a与y=b交于点D,且|BD|=3
,直线x=﹣a与y=b交于点D,且|BD|=3 ![]() ,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P.
,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P. 
(1)求椭圆的方程;
(2)证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为了了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温/℃ | 18 | 13 | 10 | -1 |
用电量/度 | 24 | 34 | 38 | 64 |
由表中数据得线性回归方程![]() 中,
中,![]() ≈-2,预测当气温为-4℃时,用电量为多少.
≈-2,预测当气温为-4℃时,用电量为多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法中,
①命题“存在x∈R,x2﹣x>0”的否定是“对于任意x∈R,x2﹣x<0”;
②命题“p且q为真”是“p或q为真”的必要不充分条件;
③已知幂函数f(x)=xα的图象经过点(2, ![]() ),则f(4)的值等于
),则f(4)的值等于 ![]() ;
;
④已知向量 ![]() =(3,﹣4),
=(3,﹣4), ![]() =(2,1),则向量
=(2,1),则向量 ![]() 在向量
在向量 ![]() 方向上的投影是
方向上的投影是 ![]() .
.
说法错误的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得![]() =80,
=80, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,  ,a=
,a=![]() -b
-b![]() ,其中
,其中![]() ,
, ![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com