已知函数
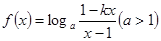
是奇函数,
(1)求
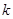
的值;
(2)在(1)的条件下判断
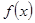
在
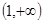
上的单调性,并运用单调性的定义予以证明.
(1)
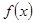
是奇函数,则
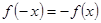
.
由
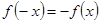
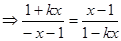
所以
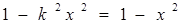
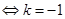
或
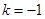
.………………………………5分
当
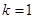
时,
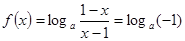
,这与题设矛盾,
当
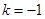
时,
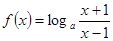
为奇函数,满足题设条件.…………………7分
(2)在(1)的条件下,
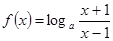
在
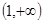
上是减函数,证明如下:
设
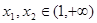
,且
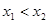
,则
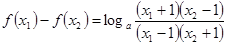
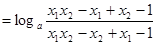
, ………………………………10分
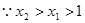
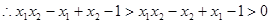
,
即
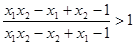
, ………………………………12分
又
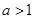
,
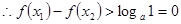
即
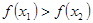
,
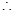
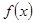
在
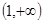
上是减函数.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
已知函数
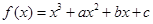
在
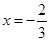
与
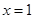
时都取得极值.若对
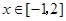
,不等式
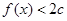
恒成立,则
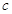
的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
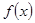
在R上单调递增,设
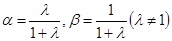
,若有
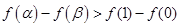
,则
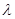
的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数

的定义域为R,对任意
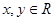
,均有
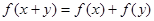
,且对任意
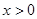
都有
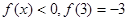
.
(1)试证明:函数

在R上是单调函数;
(2)判断

的奇偶性,并证明;
(3)解不等式
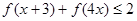
;
(4)试求函数

在
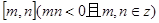
上的值域.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
如果函数
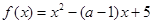
在区间
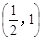
上是减函数,那么实数
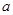
的取值范围是( ).
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设函数
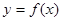
是定义在R上以
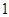
为周期的函数,若
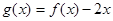
在区间
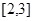
上的值域为
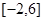
,则函数
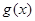
在
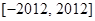
上的值域为
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数
f(
x)=
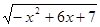
的单调增区间为( )
| A.(-∞,3] | B.[3,+∞) | C.[-1,3] | D.[3,7] |
查看答案和解析>>

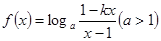 是奇函数,
是奇函数,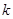 的值;
的值;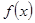 在
在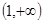 上的单调性,并运用单调性的定义予以证明.
上的单调性,并运用单调性的定义予以证明. 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 的定义域为R,对任意
的定义域为R,对任意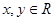 ,均有
,均有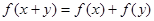 ,且对任意
,且对任意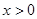 都有
都有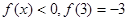 .
. 在R上是单调函数;
在R上是单调函数; 的奇偶性,并证明;
的奇偶性,并证明;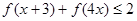 ;
; 在
在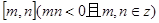 上的值域.
上的值域.