
【题目】已知数列![]() 中,
中, ![]() ,
, 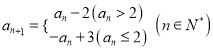 ,记
,记![]() .若
.若![]() ,则
,则![]() __________.
__________.
【答案】1343
【解析】∵a1=a(0<a2), 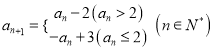 ,
,
∴a2=a1+3=3a∈[1,3).
①当a∈[1,2]时,3a∈[1,2],∴a3=a2+3=a,
∴当n=2k1,k∈N时,a1+a2=a+3a=3,
∴S2k1=3(k1)+a=2015,a=1时舍去,a=2时,k=672,此时n=1343;
当n=2k,k∈N时,a1+a2=a+3a=3,∴S2k=3k=2015,k=671+![]() ,不是整数,舍去;
,不是整数,舍去;
②当a∈(0,1)时,3a∈(2,3),∴a3=a22=1a∈(0,1),
∴a4=a3+3=a+2∈(2,3),a5=a42=a∈(2,3),
当n=4k,k∈N时, ![]() =a+3a+1a+a+2=6,
=a+3a+1a+a+2=6,
∴S4k=6k=2015,k不为整数,舍去;
当n=4k1,k∈N时, ![]() =a+3a+1a=4a,
=a+3a+1a=4a,
∴S4k1=6(k1)+(4a)=2015,舍去;
当n=4k2,k∈N时,a1+a2=3,∴S4k2=6(k1)+3=2015,舍去。
当4k3,k∈N时,∴S4k2=6(k1)+a=2015,舍去。
综上可得:n=1343.
故答案为:1343.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足a1= ![]() ,2Sn﹣SnSn﹣1=1(n≥2).
,2Sn﹣SnSn﹣1=1(n≥2).
(1)猜想Sn的表达式,并用数学归纳法证明;
(2)设bn= ![]() ,n∈N* , 求bn的最大值.
,n∈N* , 求bn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的定义域;
的定义域;
(2)若![]() 判断
判断![]() 的奇偶性;
的奇偶性;
(3)是否存在实数![]() 使函数
使函数![]() 在[2,3]递增,并且最大值为1,若存在,求出
在[2,3]递增,并且最大值为1,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com