
【题目】设![]() 为等差数列
为等差数列![]() 的公差,数列
的公差,数列![]() 的前
的前![]() 项和
项和![]() ,满足
,满足![]() (
(![]() ),且
),且![]() ,若实数
,若实数![]() (
(![]() ,
,![]() ),则称
),则称![]() 具有性质
具有性质![]() .
.
(1)请判断![]() 、
、![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,若
项和,若![]() 是单调递增数列,求证:对任意的
是单调递增数列,求证:对任意的![]() (
(![]() ,
,![]() ),实数
),实数![]() 都不具有性质
都不具有性质![]() ;
;
(3)设![]() 是数列
是数列![]() 的前
的前![]() 项和,若对任意的
项和,若对任意的![]() ,
,![]() 都具有性质
都具有性质![]() ,求所有满足条件的
,求所有满足条件的![]() 的值.
的值.
【答案】(1)![]() 不具有性质
不具有性质![]() ,
,![]() 具有性质
具有性质![]() ,理由见解析;(2)证明见解析;(3)
,理由见解析;(2)证明见解析;(3)![]() 和
和![]() .
.
【解析】
(1)求得![]() 时,数列
时,数列![]() 的前7项,可得
的前7项,可得![]() 和首项
和首项![]() ,得到等差数列
,得到等差数列![]() 的通项,即可判断
的通项,即可判断![]() 、
、![]() 是否具有性质
是否具有性质![]() ;
;
(2)由题意可得![]() ,代入等差数列
,代入等差数列![]() 的通项公式和求和公式,化简整理可得入
的通项公式和求和公式,化简整理可得入![]() ,结合集合中元素的特点,即可得证;
,结合集合中元素的特点,即可得证;
(3)求得![]() 的特点,结合
的特点,结合![]() 集合的特点,即可得到所求取值.
集合的特点,即可得到所求取值.
解:(1)由![]() 得
得![]() ,
,
又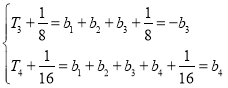 ,得
,得![]() ,
,
可得![]() ,
,
从而![]() ,
,
故![]() 不具有性质
不具有性质![]() ,
,![]() 具有性质
具有性质![]() .
.
(2)![]() ,
,
因为数列![]() 单调递增,所以
单调递增,所以![]() ,即
,即![]() ,
,
又数列![]() 单调递增,则数列
单调递增,则数列![]() 的最小项为
的最小项为![]() ,
,
则对任意![]() ,都有
,都有![]() ,
,
故实数![]() 都不具有性质
都不具有性质![]() .
.
(3)因为![]() ,所以
,所以![]() ,
,
两式相减得 ![]()
![]() ,
,
即![]()
![]() ,
,
当![]() 为偶数时,
为偶数时,![]() ,即
,即![]() ,此时
,此时![]() 为奇数;
为奇数;
当![]() 为奇数时,
为奇数时,![]() ,即
,即![]() ,则
,则![]() ,
,
此时![]() 为偶数;
为偶数;
则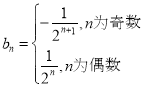 ,
,![]() .
.
则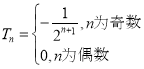 ,
,
故![]()
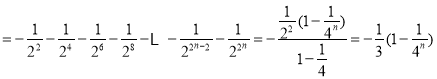 ,
,
因为![]() 对于一切
对于一切![]() 递增,所以
递增,所以![]() ,
,
所以 ![]() .
.
若对任意的![]() ,
,![]() 都具有性质
都具有性质![]() ,则
,则![]()
![]() ,
,
即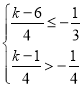 ,解得
,解得![]() ,又
,又![]() ,则
,则![]() 或
或![]() ,
,
即所有满足条件的正整数![]() 的值为
的值为![]() 和
和![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,过抛物线![]() 焦点
焦点![]() 的直线与抛物线交于
的直线与抛物线交于![]() (其中
(其中![]() 点在
点在![]() 轴的上方)两点.
轴的上方)两点.
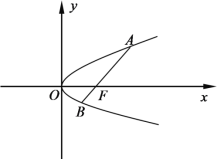
(1)若线段![]() 的长为3,求
的长为3,求![]() 到直线
到直线![]() 的距离;
的距离;
(2)证明:![]() 为钝角三角形;
为钝角三角形;
(3)已知![]() 且
且![]() ,求三角形
,求三角形![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(I)证明:CE∥平面PAB;
(II)求直线CE与平面PBC所成角的正弦值

查看答案和解析>>
科目:高中数学 来源: 题型:
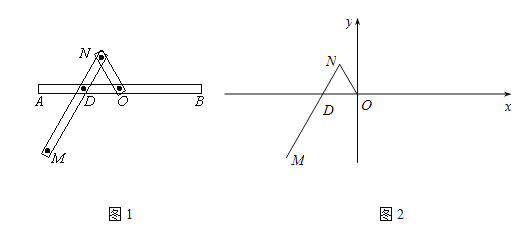
【题目】一种作图工具如图1所示.![]() 是滑槽
是滑槽![]() 的中点,短杆
的中点,短杆![]() 可绕
可绕![]() 转动,长杆
转动,长杆![]() 通过
通过![]() 处铰链与
处铰链与![]() 连接,
连接,![]() 上的栓子
上的栓子![]() 可沿滑槽AB滑动,且
可沿滑槽AB滑动,且![]() ,
,![]() .当栓子
.当栓子![]() 在滑槽AB内作往复运动时,带动
在滑槽AB内作往复运动时,带动![]() 绕
绕![]() 转动一周(
转动一周(![]() 不动时,
不动时,![]() 也不动),
也不动),![]() 处的笔尖画出的曲线记为
处的笔尖画出的曲线记为![]() .以
.以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
(Ⅰ)求曲线C的方程;
(Ⅱ)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与曲线
总与曲线![]() 有且只有一个公共点,试探究:
有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为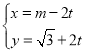 (
(![]() ,
,![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为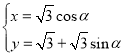 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,求曲线
轴正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月1日新修订的个税法正式实施,规定:公民全月工资、薪金所得不超过5000元的部分不必纳税,超过5000元的部分为全月应纳税所得额.此项税款按下表分段累计计算(预扣):
全月应缴纳所得额 | 税率 |
不超过3000元的部分 |
|
超过3000元至12000元的部分 |
|
超过12000元至25000元的部分 |
|
国家在实施新个税时,考虑到纳税人的实际情况,实施了《个人所得税税前专项附加扣税暂行办法》,具体如下表:
项目 | 每月税前抵扣金额(元) | 说明 |
子女教育 | 1000 | 一年按12月计算,可扣12000元 |
继续教育 | 400 | 一年可扣除4800元,若是进行技能职业教育或者专业技术职业资格教育一年可扣除3600元 |
大病医疗 | 5000 | 一年最高抵扣金额为60000元 |
住房贷款利息 | 1000 | 一年可扣除12000元,若夫妻双方在同一城市工作,可以选择一方来扣除 |
住房租金 | 1500/1000/800 | 扣除金额需要根据城市而定 |
赡养老人 | 2000 | 一年可扣除24000元,若不是独生子女,子女平均扣除.赡养老人年龄需要在60周岁及以上 |
老李本人为独生子女,家里有70岁的老人需要赡养,有一个女儿正读高三,他每月还需缴纳住房贷款2734元.若2019年11月老李工资,薪金所得为20000元,按照《个人所得税税前专项附加扣税暂行办法》,则老李应缴纳税款(预扣)为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,定义![]() 为两点
为两点![]() 、
、![]() 的“切比雪夫距离”,又设点
的“切比雪夫距离”,又设点![]() 及
及![]() 上任意一点
上任意一点![]() ,称
,称![]() 的最小值为点
的最小值为点![]() 到直线
到直线![]() 的“切比雪夫距离”,记作
的“切比雪夫距离”,记作![]() ,给出四个命题,正确的是________.
,给出四个命题,正确的是________.
①对任意三点![]() 、
、![]() 、
、![]() ,都有
,都有![]() ;
;
② 到原点的“切比雪夫距离”等于![]() 的点的轨迹是正方形;
的点的轨迹是正方形;
③ 已知点![]() 和直线
和直线![]() ,则
,则![]() ;
;
④ 定点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹与直线
的轨迹与直线![]() (
(![]() 为常数)有且仅有
为常数)有且仅有![]() 个公共点.
个公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图被称为“中华第一图”.从孔庙大成殿梁柱,到楼观台、三茅宫标记物;从道袍、卦摊、中医、气功、武术到韩国国旗![]() ,太极图无不跃居其上.这种广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极图”.在如图所示的阴阳鱼图案中,阴影部分可表示为
,太极图无不跃居其上.这种广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极图”.在如图所示的阴阳鱼图案中,阴影部分可表示为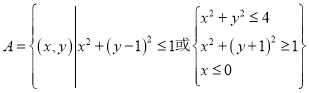 ,设点
,设点![]() ,则
,则![]() 的最大值与最小值之差是( )
的最大值与最小值之差是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点是抛物线
的右焦点是抛物线![]()
![]() 的焦点,直线
的焦点,直线![]() 与
与![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求![]() 的方程;
的方程;
(2)若直线![]() 经过点
经过点![]() ,求
,求![]() 的面积的最小值(
的面积的最小值(![]() 为坐标原点);
为坐标原点);
(3)已知点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com