练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
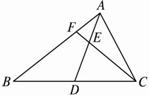
    如图1-20,已知AD是△ABC的中线,从顶点C任意引一条射线交AD于E,交AB于F.求证:AE·BF =2AF·DE.

    图1-20

    思路分析:本题证法较多,要证AE·BF =2AF·DE,?

    只需证=.?

    考虑和点D为BC的中点,?

    设想过点D构造CF的平行线交AB于点M,则BM =MF,?

    从而= =,容易证明=.

    证明:过点D作DM∥CF交AB于点M,?

    ∵BD =DC,∴BM =MF.?

    在△ADM中,∵EF∥DM,?

    ∴= = =,?

    即=.?

    从而AE·BF =2AF·DE.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

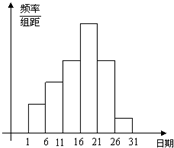    某市教育局在中学开展“创新素质实践行”小论文的评比．各校交论文的时间为5月1日至30日，评委会把各校交的论文的件数按5天一组分组统计，绘制了频率分布直方图（如图）．已知从左至右各长方形的高的比为2：3：4：6：4：1，第二组的频数为18．那么本次活动收到论文的篇数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

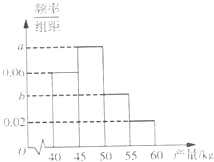    （2013•广州一模）沙糖桔是柑桔类的名优品种，因其味甜如砂糖故名，某果农选取一片山地种植沙糖桔，收获时，该果农随机选取果树20株作为样本测量它们每一株的果实产量（单位：kg），获得的所有数据按照区间（40，45]，（45，50]，（50，55]，（55，60]，进行分组，得到频率分布直方图如图3，已知样本中产量在区间（45，50]上的果树株数是产量在区间（50，60]上的果树株数的
    43
    倍．
    （1）求a，b的值；
    （2）从样本中产量在区间（50，60]上的果树随机抽取两株，求产量在区间（55，60]上的果树至少有一株被抽中的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

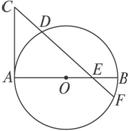
    如图2-20,已知AB是⊙O直径,AC是⊙O的切线,A为切点,割线CDF交AB于E,并且CD∶DE∶EF=1∶2∶1,AC=4,则⊙O的直径AB=_________.

    图2-20

    查看答案和解析>>

    科目：高中数学 来源： 题型：

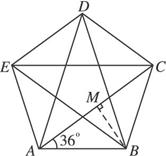
    如图所示,已知五边形ABCDE是边长为1的正五边形,在以A、B、C、D、E五点中任意两点为始点和终点的向量中，模等于2cos36°的向量个数为（    ）

    A．5                B．10                 C．15               D．20

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

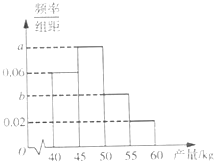    沙糖桔是柑桔类的名优品种，因其味甜如砂糖故名，某果农选取一片山地种植沙糖桔，收获时，该果农随机选取果树20株作为样本测量它们每一株的果实产量（单位：kg），获得的所有数据按照区间（40，45]，（45，50]，（50，55]，（55，60]，进行分组，得到频率分布直方图如图3，已知样本中产量在区间（45，50]上的果树株数是产量在区间（50，60]上的果树株数的数学公式倍．
    （1）求a，b的值；
    （2）从样本中产量在区间（50，60]上的果树随机抽取两株，求产量在区间（55，60]上的果树至少有一株被抽中的概率．

    查看答案和解析>>

    同步练习册答案