
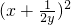 +
+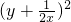 的最小值是
的最小值是

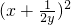 +
+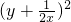 ≥2(x+
≥2(x+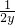 )×(y+
)×(y+ )整理得知
)整理得知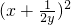 +
+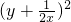 ≥2(xy+
≥2(xy+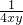 +1),其中等号成立的条件是x=y,又xy+
+1),其中等号成立的条件是x=y,又xy+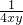 ≥2
≥2 =1等号成立的条件是xy=
=1等号成立的条件是xy=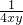 与x=y联立得两次运用基本不等式等号成立的条件是x=y=
与x=y联立得两次运用基本不等式等号成立的条件是x=y= ,计算出最值是4
,计算出最值是4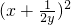 +
+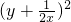 ≥2(xy+
≥2(xy+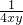 +1),
+1),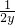 =y+
=y+ ,
,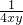 ≥2
≥2 =1
=1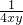 ②
② ,
, 时
时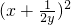 +
+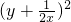 的最小值是4
的最小值是4

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com