
分析 ①中是值函数值域的交集,不是点的集合;
②函数的解析式应有意义;
③函数的奇偶性先判断定义域是否关于原点对称,再判断f(-x)与f(x)的关系;
④根据函数单调性判断方法可知
⑤第四象限的特点是x取正值时,函数值为负值.
解答 解:①若集合A={y|y=x-1},B={y|y=x2-1},则A∩B={y|y≥-1},故错误;
②y=$\sqrt{x-3}$+$\sqrt{2-x}$的定义域为空集,故不是函数解析式,故错误;
③y=$\frac{\sqrt{1{-x}^{2}}}{1-|3-x|}$的定义域为[-1,1],f(-x)≠f(x)且f(-x)≠-f(x),故是非奇非偶函数,故正确;
④若函数f(x)在(-∞,0],[0,+∞)都是单调增函数,根据递增的定义可知,f(x)在(-∞,+∞)上也是增函数,故正确;
⑤幂函数y=xα的定义可知,当x>0时,无论a为何值,函数值都大于零,故图象不经过第四象限,故正确.
故答案为:③④⑤.
点评 考查了集合的概念,函数的奇偶性,函数的单调性和幂函数的性质.


科目:高中数学 来源: 题型:选择题
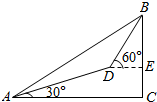 某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进1 000m后到达D处,又测得山顶的仰角为60°,则山的高度BC为( )
某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进1 000m后到达D处,又测得山顶的仰角为60°,则山的高度BC为( )| A. | 500($\sqrt{3}$+1)m | B. | 500m | C. | 500($\sqrt{2}$+1)m | D. | 1000m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{8}$ | B. | 0 | C. | $\frac{π}{8}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{5}-3$ | B. | $3\sqrt{5}-2\sqrt{2}$ | C. | $3\sqrt{2}+2$ | D. | $2\sqrt{5}+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-2x=$\frac{9}{10}$ | B. | 1-2x=$\frac{10}{11}$ | C. | (1-x)2=$\frac{9}{10}$ | D. | (1-x)2=$\frac{10}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com