
【题目】已知函数![]() 和
和![]() .
.
(1)讨论函数![]() 的奇偶性;
的奇偶性;
(2)当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的值域.
上的值域.
【答案】(1)答案见解析;(2)答案见解析.
【解析】试题分析:
(1)首先确定函数的定义域为R,然后分类讨论可得当![]() 时,
时, ![]() 为偶函数;
为偶函数;
当![]() 时,
时, ![]() 既非奇函数又非偶函数;
既非奇函数又非偶函数;
(2)结合题意和二次函数的性质可得当![]() 时,
时, ![]() 的值域为
的值域为![]() ;当
;当![]() 时,
时, ![]() 的值域为
的值域为![]() .
.
试题解析:
(1)函数![]() ,其定义域为
,其定义域为![]() ,
,
1°当![]() 时,
时, ![]() ,∵
,∵![]() ,
,
∴![]() 为偶函数;
为偶函数;
2°当![]() 时,
时, ![]() ,取
,取![]() ,
, ![]() ,
,
∵![]() ,∴
,∴![]() 且
且![]() ,∴
,∴![]() 既非奇函数又非偶函数;
既非奇函数又非偶函数;
(2)函数![]() ,其中
,其中![]() ,
,
设函数![]() ,其对称轴为
,其对称轴为![]() ,
, ![]() ,
, ![]() ,
,
1°当![]() ,即
,即![]() 时,
时, ![]() 对
对![]() 恒成立且在
恒成立且在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,
, ![]() ,
,
即![]() 的值域为
的值域为![]() ;
;
2°当![]() ,即
,即![]() 时,令
时,令![]() ,有
,有![]() (舍)和
(舍)和![]() ,
,
![]() 在
在![]() 上单调递增,且当
上单调递增,且当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,且
上递增,且![]() ,∴
,∴![]() ,
,
![]()
![]()
①当![]() ,即
,即![]() 时,
时, ![]() ,即
,即![]() 的值域为
的值域为![]() ;
;
②当![]() ,即
,即![]() 时,
时, ![]() ,即
,即![]() 的值域为
的值域为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系中, ![]() 为极点,半径为2的圆
为极点,半径为2的圆![]() 的圆心坐标为
的圆心坐标为![]() .
.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设直角坐标系的原点与极点![]() 重合,
重合, ![]() 轴非负关轴与极轴重合,直线
轴非负关轴与极轴重合,直线![]() 的参数方程为
的参数方程为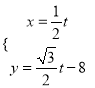 (
(![]() 为参数),由直线
为参数),由直线![]() 上的点向圆
上的点向圆![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=7,a5+a7=26.{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn=﹣ ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足a1= ![]() ,an+1﹣an+anan+1=0(n∈N*).
,an+1﹣an+anan+1=0(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:a1+a1a2+a1a2a3+…+a1a2…an<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,Sn为前n天两只老鼠打洞长度之和,则Sn=尺.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,定点
,定点![]() 为圆上一动点,线段
为圆上一动点,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() ;
;
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)若经过![]() 的直线
的直线![]() 交曲线于不同的两点
交曲线于不同的两点![]() ,(点
,(点![]() 在点
在点![]() ,
, ![]() 之间),且满足
之间),且满足![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com