
【题目】将圆 ![]() 为参数)上的每一点的横坐标保持不变,纵坐标变为原来的
为参数)上的每一点的横坐标保持不变,纵坐标变为原来的 ![]() 倍,得到曲线C.
倍,得到曲线C.
(1)求出C的普通方程;
(2)设直线l:x+2y﹣2=0与C的交点为P1 , P2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系, 求过线段P1P2的中点且与l垂直的直线的极坐标方程.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a1=1,且a1 , a2 , a4+2成等比数列.
(1)求数列{an}的通项公式及其前n项和Sn;
(2)设 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,且椭圆C上的点到椭圆右焦点F的最小距离为
,且椭圆C上的点到椭圆右焦点F的最小距离为 ![]() .
.
(1)求椭圆C的方程;
(2)过点F且不与坐标轴平行的直线l与椭圆C交于A,B两点,线段AB的中点为M, O为坐标原点,直线 ![]() 的斜率分别为
的斜率分别为 ![]() 若成等差数列,求直线l的方程.
若成等差数列,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市需对某环城快速车道进行限速,为了调研该道路车速情况,于某个时段随机对 ![]() 辆车的速度进行取样,测量的车速制成如下条形图:
辆车的速度进行取样,测量的车速制成如下条形图:
经计算:样本的平均值 ![]() ,标准差
,标准差 ![]() ,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于
,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于 ![]() 或车速大于
或车速大于 ![]() 是需矫正速度.
是需矫正速度.
(1)从该快速车道上所有车辆中任取 ![]() 个,求该车辆是需矫正速度的概率;
个,求该车辆是需矫正速度的概率;
(2) 从样本中任取
从样本中任取 ![]() 个车辆,求这
个车辆,求这 ![]() 个车辆均是需矫正速度的概率
个车辆均是需矫正速度的概率
(3)从该快速车道上所有车辆中任取 ![]() 个,记其中是需矫正速度的个数为
个,记其中是需矫正速度的个数为 ![]() ,求
,求 ![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地电影院为了了解当地影迷对快要上映的一部电影的票价的看法,进行了一次调研,得到了票价x(单位:元)与渴望观影人数y(单位:万人)的结果如下表:
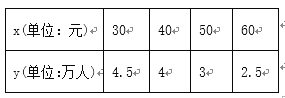
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)根据(1)中求出的线性回归方程,若票价定为70元,预测该电影院渴望观影人数.附:回归直线的斜率和截距的最小二乘法估计公式分别为: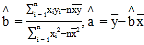
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n(n∈N*)项和为Sn , a3=3,且λSn=anan+1 , 在等比数列{bn}中,b1=2λ,b3=a15+1. (Ⅰ)求数列{an}及{bn}的通项公式;
(Ⅱ)设数列{cn}的前n(n∈N*)项和为Tn , 且 ![]() ,求Tn .
,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设D为不等式组  ,表示的平面区域,点B(a,b)为第一象限内一点,若对于区域D内的任一点A(x,y)都有
,表示的平面区域,点B(a,b)为第一象限内一点,若对于区域D内的任一点A(x,y)都有 ![]() 成立,则a+b的最大值等于( )
成立,则a+b的最大值等于( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com