
分析 由新定义可得数列a2,$\sqrt{{y}^{2}-1}$,x2-1为等比数列,进一步得到$\frac{{x}^{2}}{\frac{{a}^{2}-1}{{a}^{2}}}-\frac{{y}^{2}}{{a}^{2}-1}=1$,由此可得$\frac{{x}^{2}}{\frac{{a}^{2}-1}{{a}^{2}}}≤1$,即${x}^{2}≤\frac{{a}^{2}-1}{{a}^{2}}$,再转化为只含a的代数式,配方后利用基本不等式求最值.
解答 解:由题意,数列a2,$\sqrt{{y}^{2}-1}$,cos$\frac{π}{2}$,x2-1为“弱等比数列”,
则数列a2,$\sqrt{{y}^{2}-1}$,x2-1为等比数列,
∴y2-1=a2(x2-1),
即a2x2-y2=a2-1,
由题意可知,a>1,
∴$\frac{{x}^{2}}{\frac{{a}^{2}-1}{{a}^{2}}}-\frac{{y}^{2}}{{a}^{2}-1}=1$,
则$\frac{{x}^{2}}{\frac{{a}^{2}-1}{{a}^{2}}}≤1$,∴${x}^{2}≤\frac{{a}^{2}-1}{{a}^{2}}$,
则$\frac{{a}^{2}}{{x}^{2}}≥\frac{{a}^{4}}{{a}^{2}-1}$=$\frac{({a}^{2}-1)^{2}+2({a}^{2}-1)+1}{{a}^{2}-1}$=$({a}^{2}-1)+\frac{1}{{a}^{2}-1}+2≥4$,
当且仅当${a}^{2}-1=\frac{1}{{a}^{2}-1}$,即a=2(a>1)时取等号.
∴$\frac{a}{x}≥2$(a>1,x>1).
即$\frac{a}{x}$的最小值为2.
故答案为:2.
点评 本题考查数列递推式,考查了数列的函数特性,训练了利用基本不等式求最值,是难题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
 如图,在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连结BC1,过B1作B1E⊥BC1交CC1于点E.
如图,在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连结BC1,过B1作B1E⊥BC1交CC1于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}-\frac{y^2}{27}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{27}=1$ | C. | $\frac{y^2}{27}-\frac{x^2}{9}=1$ | D. | $\frac{x^2}{27}-\frac{y^2}{9}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
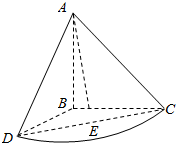 等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:
等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
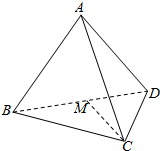 如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.
如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com