
【题目】设正项数列{an}的前n项和为Sn , 且a ![]() +2an=4Sn(n∈N*).
+2an=4Sn(n∈N*).
(1)求an;
(2)设数列{bn}满足:b1=1,bn= ![]() (n∈N* , n≥2),求数列{bn}的前n项和Tn .
(n∈N* , n≥2),求数列{bn}的前n项和Tn .
【答案】
(1)解:当n=1时,a12+2a1=4S1=4a1,
解得a1=2,
当n>1时,an﹣12+2an﹣1=4Sn﹣1,
又a ![]() +2an=4Sn(n∈N*).
+2an=4Sn(n∈N*).
两式相减可得,a ![]() ﹣an﹣12+2an﹣2an﹣1=4Sn﹣4Sn﹣1=4an,
﹣an﹣12+2an﹣2an﹣1=4Sn﹣4Sn﹣1=4an,
即有(an﹣an﹣1)(an+an﹣1)=2(an+an﹣1),
可得an﹣an﹣1=2,
则an=a1+2(n﹣1)=2n:
(2)解:b1=1,bn= ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
前n项和Tn=1+ ![]() (
( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() )
)
=1+ ![]() (
( ![]() +
+ ![]() ﹣﹣
﹣﹣ ![]() ﹣
﹣ ![]() )
)
= ![]() ﹣
﹣ ![]()
![]() .
.
【解析】(1)令n=1,求得首项为2;再由n>1时,将n换为n﹣1,相减可得an﹣an﹣1=2,再由等差数列的通项公式,计算即可得到所求;(2)求得bn= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),运用数列的求和方法:裂项相消求和,化简整理即可得到所求和.
),运用数列的求和方法:裂项相消求和,化简整理即可得到所求和.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD与ABEF均为矩形,BC=BE=2AB,二面角E﹣AB﹣C的大小为 ![]() .现将△ACD绕着AC旋转一周,则在旋转过程中,( )
.现将△ACD绕着AC旋转一周,则在旋转过程中,( ) 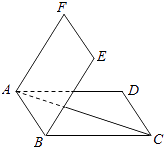
A.不存在某个位置,使得直线AD与BE所成的角为 ![]()
B.存在某个位置,使得直线AD与BE所成的角为 ![]()
C.不存在某个位置,使得直线AD与平面ABEF所成的角为 ![]()
D.存在某个位置,使得直线AD与平面ABEF所成的角为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+2bx+c,设函数g(x)=|f(x)|在区间[﹣1,1]上的最大值为M.
(1)若b=2,试求出M;
(2)若M≥k对任意的b、c恒成立,试求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对应的边分别为a,b,c,且(2a﹣c)cosB=bcosC. (Ⅰ)求角B的大小;
(Ⅱ)若a=2,c=3,求sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形BCEF所成角的二面角的平面角的大小是 ![]() ,PQ是正方形BDEF所在平面内的一条动直线,则直线BD与PQ所成角的取值范围是( )
,PQ是正方形BDEF所在平面内的一条动直线,则直线BD与PQ所成角的取值范围是( ) 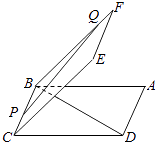
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=3sin(4x+ ![]() )图象上所有点的横坐标伸长到原来的2倍,再向右平移
)图象上所有点的横坐标伸长到原来的2倍,再向右平移 ![]() 个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
A.x= ![]()
B.x= ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的方程为(x﹣3)2+y2=1,圆M的方程为(x﹣3﹣3cosθ)2+(y﹣3sinθ)2=1(θ∈R),过M上任意一点P作圆C的两条切线PA,PB,切点分别为A、B,则∠APB的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x﹣ ![]() sin2x+asinx在(﹣∞,+∞)单调递增,则a的取值范围是( )
sin2x+asinx在(﹣∞,+∞)单调递增,则a的取值范围是( )
A.[﹣1,1]
B.[﹣1, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣1,﹣ ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com