
分析 (I)求出函数的导数,求得切线的斜率和切点,由点斜式方程,可得切线方程;
(II)由题意可得当x∈[0,+∞)时,ax2+ln(x+1)≤x,构造g(x)=ax2+ln(x+1)-x,求得导数,判断单调性,对a讨论,得到g(x)≤0恒成立的a的范围;
(Ⅲ)令g(x)=ln(x+1)-2x(x≥0),求出导数,判断单调性,再令x=$\frac{1}{n(n+2)}$,则ln(1+$\frac{1}{n(n+2)}$)<$\frac{2}{n(n+2)}$=$\frac{1}{n}$-$\frac{1}{n+2}$,再由裂项相消求和,以及不等式的性质,即可得证.
解答 (I)解:f′(x)=2ax+$\frac{1}{x+1}$,
则切线的斜率为f′(0)=1,又f(0)=0,
∴f(x)在(0,f(0))处切线方程为y=x;
(II)解:∵当x∈[0,+∞),f(x)上的点均在$\left\{\begin{array}{l}x≥0\\ y-x≤0\end{array}$表示的区域内,
∴当x∈[0,+∞)时,ax2+ln(x+1)≤x,
即g(x)=ax2+ln(x+1)-x≤0,
g′(x)=2ax+$\frac{1}{x+1}$-1=2ax-$\frac{x}{x+1}$.
当a≤0时,g′(x)≤0,
∴函数g(x)在[0,+∞)上单调递减,
∴g(x)≤g(0)=0,满足题意,因此a≤0适合条件;
当a>0时,g′(x)=$\frac{2ax(x-\frac{1-2a}{2a})}{x+1}$.
当a≥$\frac{1}{2}$时,g′(x)≥0,函数g(x)在[0,+∞)上单调递增,
g(x)≥0,不满足题意,舍去;
当$0<a<\frac{1}{2}$时,令g′(x)>0,解得$x>\frac{1-2a}{2a}$,
此时函数g(x)单调递增;令g′(x)<0,
解得$0<x<\frac{1-2a}{2a}$,此时函数g(x)单调递减.
∴$g(\frac{1-2a}{2a})$<g(0)=0,
不满足题意,舍去.
综上可得:实数a的取值范围是(-∞,0].
(Ⅲ)证明:令h(x)=ln(x+1)-2x(x≥0),
则h′(x)=$\frac{1}{x+1}$-2=$\frac{-1-2x}{x+1}$<0,
h(x)在[0,+∞)递减,
即有h(x)≤h(0)=0,
则ln(x+1)≤2x,
令x=$\frac{1}{n(n+2)}$,
则ln(1+$\frac{1}{n(n+2)}$)<$\frac{2}{n(n+2)}$=$\frac{1}{n}$-$\frac{1}{n+2}$,
即有$\sum_{i=1}^{n}\frac{(i+1)^{2}}{i(i+2)}$=$\sum_{i=1}^{n}$(1+$\frac{1}{i(i+2)}$)<(1-$\frac{1}{3}$)+($\frac{1}{2}$-$\frac{1}{4}$)+…+($\frac{1}{n-1}$-$\frac{1}{n+1}$)+($\frac{1}{n}$-$\frac{1}{n+2}$)
=1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$<$\frac{3}{2}$.
故原不等式成立.
点评 此题主要考查利用导数研究切线方程和函数的单调区间和最值问题,解题过程中多次用到了转化的思想,函数的恒成立问题转化为求最值问题,同时考查不等式的证明,注意运用函数的单调性和裂项相消求和,本题难度比较大,是一道综合题.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
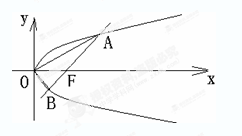 过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.
过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 有5位工人在某天生产同一零件,所生产零件个数的茎叶图如图所示,已知它们生产零件的平均数为10,标准差为$\sqrt{2}$,则|x-y|的值为( )
有5位工人在某天生产同一零件,所生产零件个数的茎叶图如图所示,已知它们生产零件的平均数为10,标准差为$\sqrt{2}$,则|x-y|的值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com