
| 6 |

| CF2+FA2 |
| 3+3 |
| 6 |


科目:高中数学 来源:江西省临川一中2010-2011学年高一3月月考数学试题 题型:022
将边长为2,有一内角为60°的菱形ABCD沿较短对角线BD折成四面体A-
BCD,点E、F分别为AC、BD的中点,则下列命题中正确的是________(将正确的命题序号全填上):①![]() ;
;
②EF与异面直线AC、BD都垂直;
③当四面体ABCD的体积最大时,![]() ;
;
④AC垂直于截面BDE.
查看答案和解析>>
科目:高中数学 来源:山东省期中题 题型:填空题
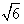 ;④AC垂直于截面BDE。
;④AC垂直于截面BDE。 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com