
分析 (1)根据函数f(x)展开式中x2的系数列出方程${C}_{n+1}^{2}$+${C}_{n}^{2}$=25,求出n的值;
(2)(ⅰ)赋值法:分别令x=1和x=-1,两式相加求出a0+a2+a4+a6的值;
(ⅱ)赋值法:令x=$\frac{1}{2}$和x=0,即可求出$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{7}}{{2}^{7}}$的值.
解答 解:(1)函数f(x)=(1-x)m+(1-x)n,
当m=n+1时,f(x)展开式中x2的系数是
${C}_{n+1}^{2}$+${C}_{n}^{2}$=25,
即$\frac{1}{2}$n(n+1)+$\frac{1}{2}$n(n-1)=25,
解得n=±5,
应取n=5; …(4分)
(2)(ⅰ)赋值法:令x=1,得f(1)=a7+a6+…+a1+a0,
令x=-1,得f(-1)=-a7+a6-…-a1+a0;
则f(1)+f(-1)=2(a6+a4+a2+a0)=2×27=256,
所以a0+a2+a4+a6=128;------(8分)
(ⅱ)赋值法:令x=$\frac{1}{2}$,a0+$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{7}}{{2}^{7}}$=2×${(\frac{1}{2})}^{7}$=$\frac{1}{64}$;
x=0,a0=1+1=2,
因此)$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{7}}{{2}^{7}}$=$\frac{1}{64}$-2=-$\frac{127}{64}$.------(12分)
点评 本题考查了二项式定理的应用问题,也考查了利用赋值法求对应项的系数问题,是综合性题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{16\sqrt{3}}}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $8\sqrt{3}$ | D. | $16\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
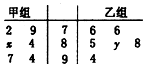 如图叶茎图记录了甲、乙两组各6名学生在一次数字测试中的成绩(单位:分),已知甲组数据的众数为84,乙组数据的平均数即为甲组数据的中位数,则x,y的值分别为( )
如图叶茎图记录了甲、乙两组各6名学生在一次数字测试中的成绩(单位:分),已知甲组数据的众数为84,乙组数据的平均数即为甲组数据的中位数,则x,y的值分别为( )| A. | 4,5 | B. | 5,4 | C. | 4,4 | D. | 5,5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36种 | B. | 72种 | C. | 144种 | D. | 288种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
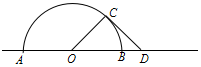 某公园内直线道路旁有一半径为10米的半圆形荒地(圆心O在道路上,AB为直径),现要在荒地的基础上改造出一处景观.在半圆上取一点C,道路上B点的右边取一点D,使OC垂直于CD,且OD的长不超过20米.在扇形区域AOC内种植花卉,三角形区域OCD内铺设草皮.已知种植花卉的费用每平方米为200元,铺设草皮的费用每平方米为100元.
某公园内直线道路旁有一半径为10米的半圆形荒地(圆心O在道路上,AB为直径),现要在荒地的基础上改造出一处景观.在半圆上取一点C,道路上B点的右边取一点D,使OC垂直于CD,且OD的长不超过20米.在扇形区域AOC内种植花卉,三角形区域OCD内铺设草皮.已知种植花卉的费用每平方米为200元,铺设草皮的费用每平方米为100元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com