
【题目】已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(﹣1,0)上与函数f(x)的单调性相同的是( )

A.![]() B.y=log2|x|
B.y=log2|x|
C. D.y=cos(2x)
D.y=cos(2x)
【答案】D
【解析】
根据题意,由函数奇偶性的性质分析可得y=f(x)在(﹣1,0)上单调递增,据此依次分析选项中函数在区间(﹣1,0)上的单调性,即可得答案.
解:根据图象可以判断出(0,1)单调递增,又由函数y=f(x)(x∈R)是奇函数,
则函数y=f(x)在(﹣1,0)上单调递增,
依次分析选项:
对于A、对于y=x![]() ,y′=1
,y′=1![]() ,当﹣1<x<0时,y′<0,则f(x)在(﹣1,0)是减函数,不符合题意,
,当﹣1<x<0时,y′<0,则f(x)在(﹣1,0)是减函数,不符合题意,
对于B、当﹣1<x<0时,y=log2|x|=log2(﹣x),令t=﹣x,则y=log2t,t=﹣x在(﹣1,0)为减函数,而y=log2t为增函数,则y=log2|x|在(﹣1,0)是减函数,不符合题意,
对于C、当﹣1<x<0时,y=e﹣x=(![]() )x,而0
)x,而0![]() 1,则y=e﹣x在(﹣1,0)为减函数,不符合题意,
1,则y=e﹣x在(﹣1,0)为减函数,不符合题意,
对于D、y=cos(2x),当﹣1<x<0,则有﹣2<2x<0,y=cos(2x)为增函数,符合题意;
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某地政府为改善居民的住房条件,集中建设一批经适楼房.用了1400万元购买了一块空地,规划建设8幢楼,要求每幢楼的面积和层数等都一致,已知该经适房每幢楼每层建筑面积均为250平方米,第一层建筑费用是每平方米3000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加80元.
(1)若该经适楼房每幢楼共![]() 层,总开发费用为
层,总开发费用为![]() 万元,求函数
万元,求函数![]() 的表达式(总开发费用=总建筑费用+购地费用);
的表达式(总开发费用=总建筑费用+购地费用);
(2)要使该批经适房的每平方米的平均开发费用最低,每幢楼应建多少层?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 经过点
经过点![]() ,曲线
,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(1)求曲线![]() 的普通方程,曲线
的普通方程,曲线![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上两点,当
上两点,当![]() 时,求
时,求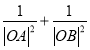 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 和
和![]() 均是等腰直角三角形,
均是等腰直角三角形,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
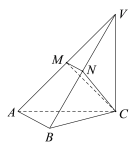
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<![]() )的部分图象如图所示.
)的部分图象如图所示.
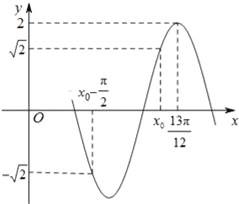
(Ⅰ)写出函数f(x)的解析式及x0的值;
(Ⅱ)求函数f(x)在区间[﹣![]() ,
,![]() ]上的最大值与最小值.
]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是定义在
是定义在![]() 上的奇函数,对
上的奇函数,对![]() ,均有
,均有![]() ,已知当
,已知当![]() 时,
时, ![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A. ![]() 的图象关于
的图象关于![]() 对称 B.
对称 B. ![]() 有最大值1
有最大值1
C. ![]() 在
在![]() 上有5个零点 D. 当
上有5个零点 D. 当![]() 时,
时, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,如果存在给定的实数对
,如果存在给定的实数对![]() ,使得
,使得![]() 恒成立,则称
恒成立,则称![]() 为“
为“![]() 函数”;
函数”;
(1)判断函数![]() ,
,![]() 是否是“
是否是“![]() 函数”;
函数”;
(2)若![]() 是一个“
是一个“![]() 函数”,求出所有满足条件的有序实数对
函数”,求出所有满足条件的有序实数对![]() ;
;
(3)若定义域为![]() 的函数
的函数![]() 是“
是“![]() 函数”,且存在满足条件的有序实数对
函数”,且存在满足条件的有序实数对![]() 和
和![]() ,当
,当![]() 时,
时,![]() 的值域为
的值域为![]() ,求当
,求当![]() 时
时![]() 的值域;
的值域;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老年人120人,中年人360人,青年人n人,为调查身体健康状况,需要从中抽取一个容量为m的样本,用分层抽样的方法进行抽样调查,样本中的中年人为6人,则n和m的值不可以是下列四个选项中的哪组( )
A.n=360,m=14B.n=420,m=15C.n=540,m=18D.n=660,m=19
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com